题目内容
9.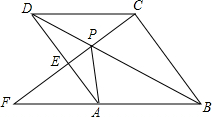 如图,点P是菱形ABCD的对角线BD上一点,连接CP并延长交AD于E,交BA的延长线于点F.
如图,点P是菱形ABCD的对角线BD上一点,连接CP并延长交AD于E,交BA的延长线于点F.(1)求证:△APD≌△CPD;
(2)求证:△APE∽△FPA;
(3)猜想:线段PC,PE,PF之间存在什么关系?并说明理由.
分析 (1)由菱形的性质得到判定△APD≌△CPD的条件;
(2)由△APD≌△CPD判断出△APE∽△FPA;
(3)由△APE∽△FPA得到$\frac{PA}{PE}=\frac{PF}{PA}$,再等量代换即可.
解答 (1)证明:∵ABCD是菱形,
∴DA=DC,∠ADP=∠CDP
在△APD和△CPD中,
$\left\{\begin{array}{l}{DA=DC}\\{∠ADP=CDP}\\{DP=DP}\end{array}\right.$,
∴△APD≌△CPD;
(2)证明:由(1)△APD≌△CPD,
得:∠PAE=∠PCD,
又由DC∥FB得:∠PFA=∠PCD
∴∠PAE=∠PFA
又∵∠APE=∠APF,
∴△APE∽△FPA
(3)解:线段PC、PE、PF之间的关系是:PC2=PE•PF,
∵△APE∽△FPA,
∴$\frac{PA}{PE}=\frac{PF}{PA}$,
∴PA2=PE•PF,
又∵PC=PA,
∴PC2=PE•PF.
点评 本题是相似图形的性质和判定,主要考查了全等三角形和相似三角形的性质和判定,解本题的关键是找到相似的三角形.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
17.八(6)班组织了一次经典朗读比赛,甲、乙两队各9人的比赛成绩如表(10分制):
(1)甲队成绩的中位数是10分,乙队成绩的众数是9分;
(2)计算乙队的平均成绩和方差;
(3)若选择其中一队参加校级经典朗读比赛则应选乙队.
| 甲 | 7 | 8 | 9 | 7 | 10 | 10 | 10 | 10 | 10 |
| 乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 |
(2)计算乙队的平均成绩和方差;
(3)若选择其中一队参加校级经典朗读比赛则应选乙队.
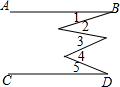 如图,AB∥CD,请猜想∠1、∠2、∠3、∠4、∠5的关系∠1+∠3+∠5=∠2+∠4.
如图,AB∥CD,请猜想∠1、∠2、∠3、∠4、∠5的关系∠1+∠3+∠5=∠2+∠4.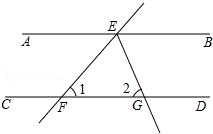 如图,AB∥CD,直线EF交AB于点E,交CD于点F,EG平分∠BEF,交CD于点G,∠1=50°,则∠2等于( )
如图,AB∥CD,直线EF交AB于点E,交CD于点F,EG平分∠BEF,交CD于点G,∠1=50°,则∠2等于( )