题目内容
2. 如图,线段AB边长为1个单位长度的正方形分割为两个等腰直角三角形,以A为圆心,AB的长为半径画弧交数轴于点C,那么点C在数轴上表示的实数是( )
如图,线段AB边长为1个单位长度的正方形分割为两个等腰直角三角形,以A为圆心,AB的长为半径画弧交数轴于点C,那么点C在数轴上表示的实数是( )| A. | 1+$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{2}-1$ | D. | 1 |
分析 先根据勾股定理求出直角三角形的斜边,即可得出选项.
解答 解:C点表示的数是:$\sqrt{{1}^{2}+{1}^{2}}$+1=$\sqrt{2}$+1=1+$\sqrt{2}$,
故选A.
点评 本题考查了数轴和实数,勾股定理的应用,能读懂图象是解此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.下列实数中,为无理数的是( )
| A. | -$\frac{3}{7}$ | B. | $\sqrt{9}$ | C. | $\root{3}{-8}$ | D. | π |
6.x取下列各数中的哪个数时,式子$\sqrt{x-3}$在实数范围内有意义( )
| A. | -2 | B. | 0 | C. | 2 | D. | 4 |
10.下列说法不正确的是( )
| A. | 用一个平面去截一个正方体可能截得五边形 | |
| B. | 五棱柱有10个顶点 | |
| C. | 沿直角三角形某条边所在的直线旋转一周,所得的几何体为圆柱 | |
| D. | 将折起的扇子打开,属于“线动成面”的现象 |
14.下列计算中,正确的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 3$\sqrt{2}$-$\sqrt{2}$=3 | C. | $\sqrt{4\frac{1}{4}}$=2$\frac{1}{2}$ | D. | $\sqrt{(-3)^{2}}$=3 |
11.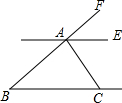 如图,已知AE∥BC,AC⊥AB,若∠ACB=50°,则∠FAE的度数是( )
如图,已知AE∥BC,AC⊥AB,若∠ACB=50°,则∠FAE的度数是( )
 如图,已知AE∥BC,AC⊥AB,若∠ACB=50°,则∠FAE的度数是( )
如图,已知AE∥BC,AC⊥AB,若∠ACB=50°,则∠FAE的度数是( )| A. | 50° | B. | 60° | C. | 40° | D. | 30° |
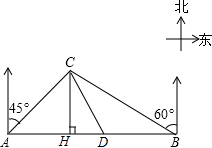 川西某高原上有一条笔直的公路,在紧靠公路相距40千米的A、B两地,分别有甲、乙两个医疗站,如图,在A地北偏东45°,B地北偏西60°方向上有一牧民区C,过点C作CH⊥AB于H.
川西某高原上有一条笔直的公路,在紧靠公路相距40千米的A、B两地,分别有甲、乙两个医疗站,如图,在A地北偏东45°,B地北偏西60°方向上有一牧民区C,过点C作CH⊥AB于H. 已知a、b、c在数轴上的位置如图,化简:|a|+|c-b|-|c|.
已知a、b、c在数轴上的位置如图,化简:|a|+|c-b|-|c|.