题目内容
2. 如图,在△ABC中,∠ACB=90°,BC=AC=4,M为AB中点,D是射线BC上一动点,连接AD,将线段AD绕点A逆时针旋转90°得到线段AE,连接ED、ME,点D在运动过程中ME的最小值为( )
如图,在△ABC中,∠ACB=90°,BC=AC=4,M为AB中点,D是射线BC上一动点,连接AD,将线段AD绕点A逆时针旋转90°得到线段AE,连接ED、ME,点D在运动过程中ME的最小值为( )| A. | 2 | B. | 2$\sqrt{2}$ | C. | 4 | D. | 4$\sqrt{2}$ |
分析 连接EB,过点M作MG⊥EB于点G,过点A作AK⊥AB交BD的延长线于点K,则△AKB是等腰直角三角形.推出△ADK≌△ABE,根据全等三角形的性质得到∠ABE=∠K=45°,证得△BMG是等腰直角三角,求出BC=4,AB=4$\sqrt{2}$,MB=2$\sqrt{2}$,由ME≥MG,于是得到当ME=MG时,ME的值最小.
解答 解:连接EB,过点M作MG⊥EB于点G,过点A作AK⊥AB交BD的延长线于点K,则△AKB是等腰直角三角形.
在△ADK与△ABE中,
$\left\{\begin{array}{l}{AK=AB}\\{∠KAD=∠BAE}\\{AD=AE}\end{array}\right.$
∴△ADK≌△ABE,
∴∠ABE=∠K=45°,
∴△BMG是等腰直角三角形,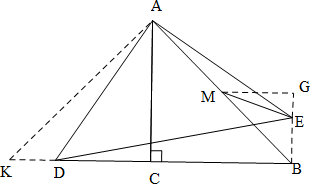
∵BC=4,
∴AB=4$\sqrt{2}$,BM=2$\sqrt{2}$,
∴MG=2,∠G=90°
∴BM≥MG,
∴当ME=MG时,ME的值最小,
∴ME=BE=2
故选:A
点评 本题证明线段最短有一点的难度.但通过构造全等三角形,利用全等三角形和直角三角形的性质就变得容易.

练习册系列答案
相关题目
20.下列各方程中,是二元一次方程的是( )
| A. | 2x-1=1+x | B. | x+1=2xy | C. | $\frac{1}{x}+y=1$ | D. | x+2y-1=0 |
7.直角三角形中有两边的长为3和4,那么第三边的长有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
14.估算$\sqrt{76}$-$\sqrt{19}$的值在相邻整数( )之间.
| A. | 4和5 | B. | 5和6 | C. | 6和7 | D. | 7和8 |
10.下列式子中,不属于代数式的是( )
| A. | a+3 | B. | mn2 | C. | $\sqrt{6}$ | D. | x>y |
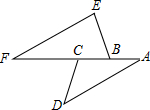 如图,已知点A、B、C、F在同一条直线上,AD∥EF,∠D=40°,∠F=30°,那么∠ACD的度数是110°.
如图,已知点A、B、C、F在同一条直线上,AD∥EF,∠D=40°,∠F=30°,那么∠ACD的度数是110°.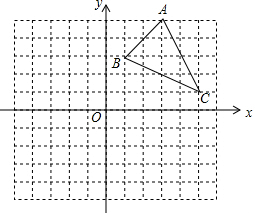 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(5,1).
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(5,1).