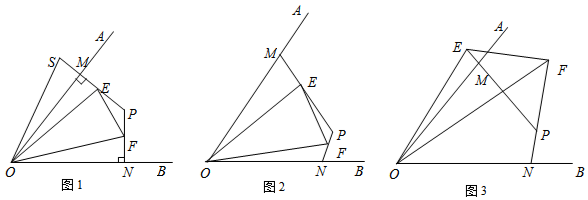
题目内容
2.(1)如图1,点M、N分别在∠AOB的边OA、OB上,且OM=ON,过点M、N分别作MP⊥OA、NP⊥OB,MP、NP交于P,E、F分别为线段MP、NP上的点,且∠EOF=$\frac{1}{2}$∠AOB,延长PM到S,使MS=NF,连接OS.则∠EOF与∠EOS的数量关系为相等,线段NF、EM、EF的数量关系为EF=NF+EM;(2)如图2,点M、N分别在∠AOB的边OA、OB上,且OM=ON,∠OMP+∠ONP=180°,E、F分别为线段MP、NP上的点,且∠EOF=$\frac{1}{2}$∠AOB,(1)中的线段NF、EM、EF的数量关系是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.
(3)如图3,点M、N分别在∠AOB的边OA、OB上,且OM=ON,∠OMP+∠ONP=180°,E、F分别为线段PM、NP延长线上的点,且∠EOF=$\frac{1}{2}$∠AOB,(1)中线段NF、EM、EF的数量关系是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.
分析 (1)结论:相等,EF=FN+EM.先证明△OMS≌△ONF,再证明△OES≌△OEF即可解决问题.
(2)结论:EF=FN+EM.如图2中,延长EM到S,使得SM=FN,连接SO,先证明△OMS≌△ONF,再证明△OES≌△OEF即可解决问题.
(3)结论:EF=FN-EM.如图3中,延长ME到S,使得MS=FN,连接SO,先证明△OMS≌△ONF,再证明△OES≌△OEF即可解决问题.
解答 解:(1)结论:相等,EF=FN+EM.
理由:如图1中,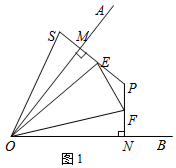
在△OMS和△ONF中,
$\left\{\begin{array}{l}{OM=ON}\\{∠OMS=∠ONF}\\{MS=FN}\end{array}\right.$,
∴△OMS≌△ONF,
∴OS=OF,∠SOM=∠FON,
∵∠EOF=$\frac{1}{2}$∠MON=∠EOM+∠FON=∠EOM+∠SOM=∠SOE,
在△OES和△OEF中,
$\left\{\begin{array}{l}{OE=OE}\\{∠SOE=∠EOF}\\{OS=OF}\end{array}\right.$,
∴△OES≌△OEF,
∴EF=SE=SM+EM=FN+EM.
故答案为相等,EF=FN+EM.
(2)如图2中,延长EM到S,使得SM=FN,连接SO.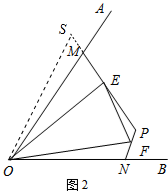
∵∠OMP+∠ONP=180°,∠OMS+∠OMP=180°,
∴∠OMS=∠ONF,
在△OMS和△ONF中,
$\left\{\begin{array}{l}{OM=ON}\\{∠OMS=∠ONF}\\{MS=FN}\end{array}\right.$,
∴△OMS≌△ONF,
∴OS=OF,∠SOM=∠FON,
∵∠EOF=$\frac{1}{2}$∠MON=∠EOM+∠FON=∠EOM+∠SOM=∠SOE,
在△OES和△OEF中,
$\left\{\begin{array}{l}{OE=OE}\\{∠SOE=∠EOF}\\{OS=OF}\end{array}\right.$,
∴△OES≌△OEF,
∴EF=SE=SM+EM=FN+EM.
(3)结论:EF=FN-EM.
理由:如图3中,延长ME到S,使得MS=FN,连接SO.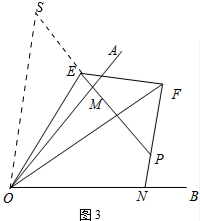
∵∠OMP+∠ONP=180°,∠OMS+∠OMP=180°,
∴∠OMS=∠ONF,
在△OMS和△ONF中,
$\left\{\begin{array}{l}{OM=ON}\\{∠OMS=∠ONF}\\{MS=FN}\end{array}\right.$,
∴△OMS≌△ONF,
∴OS=OF,∠SOM=∠FON,
∵∠EOF=$\frac{1}{2}$∠MON=∠EOM+∠FON=∠EOM+∠SOM=∠SOE,
在△OES和△OEF中,
$\left\{\begin{array}{l}{OE=OE}\\{∠SOE=∠EOF}\\{OS=OF}\end{array}\right.$,
∴△OES≌△OEF,
∴EF=SE=SM-EM=FN-EM.
点评 本题考查三角形综合题、全等三角形的判定和性质等知识,解题的关键是熟练掌握全等三角形的判定和性质,学会添加常用辅助线,构造全等三角形,属于中考常考题型.

 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | 2x-1=1+x | B. | x+1=2xy | C. | $\frac{1}{x}+y=1$ | D. | x+2y-1=0 |
| A. | 0.215×104 | B. | 2.15×103 | C. | 2.15×104 | D. | 21.5×102 |
 如图,直线AB、CD相交于点O,OM平分∠BOD,ON平分∠BOC,∠1:∠2=7:1,求∠BOD和∠AON的度数.
如图,直线AB、CD相交于点O,OM平分∠BOD,ON平分∠BOC,∠1:∠2=7:1,求∠BOD和∠AON的度数.
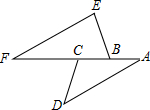 如图,已知点A、B、C、F在同一条直线上,AD∥EF,∠D=40°,∠F=30°,那么∠ACD的度数是110°.
如图,已知点A、B、C、F在同一条直线上,AD∥EF,∠D=40°,∠F=30°,那么∠ACD的度数是110°.