题目内容
如图所示，已知OC平分∠AOB，CD∥OB，若OD＝3cm，则CD等于( )
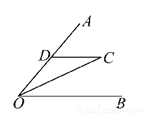
A. 3cm B. 4cm C. 1.5cm D. 2cm
A
【解析】试题分析：根据角平分线的性质可得：∠DOC=∠COB，根据平行线的性质可得：∠DCO=∠COB，则∠DOC=∠DCO，则CD=OD=3cm，故选A．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
抛物线y=2x2+4x+m与x轴只有一个公共点，则m的值为____
2
【解析】∵抛物线与x轴只有一个公共点，
∴△=0，
∴b2-4ac=42-4×2×m=0；
∴m=2．
故答案为：2. 在△ABC中，AB =AC，∠A=80°，则∠B=__________.
50°
【解析】∵AB=AC，
∴根据轴对称的性质，将线段BC对折重合后，点A在折痕上，
∴线段AB、AC关于折痕轴对称，
设折痕与BC交点为D，
则△ABD、△ACD关于直线AD轴对称，
∴∠B=∠C =(180°－∠A)÷2=（180°－80°)÷2=50°.
故答案为：50°. 下面四个图形中，不是轴对称图形的是（ ）
A. 有一个内角为45度的直角三角形 B. 有一个内角为60度的等腰三角形
C. 有一个内角为30度的直角三角形 D. 两个内角分别为36度和72度的三角形
C
【解析】A.有一个内角为45度的直角三角形，三个内角分别是45°、90°、45°，是等腰三角形，是轴对称图形；
B.有一个内角为60°的等腰三角形，三个角度数分别为60°、60°、60°，是等边三角形，是轴对称图形；对于C，有一个内角为30度的直角三角形，三个角度数分别为30°、90°、60°，不是等腰三角形，不是轴对称图形；
D.两个内角分别为36度和72度的三角形，三个角... 用反证法证明命题“对顶角相等”第一步假设__________________.
对顶角不相等
【解析】试题分析：利用反证法来进行证明时，首先假设结论不成立，即先假设“对顶角不相等”． 如图所示，某货船以20海里／时的速度将一批重要物资由A处运往正西方向的B处，经16小时到达，到达后立即卸货，此时接到气象部门通知，一台风中心正以40海里／时的速度由A处向北偏西60°的AC方向移动，距台风中心200海里的圆形区域(包括边界)均会受到影响：
(1)B处是否会受到台风的影响?清说明理由；
(2)为避免卸货过程受到台风影响，船上人员应在多少小时内卸完货物?(精确到0.1小时，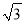 
≈1.732)
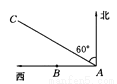
（1）B处会受到台风的影响（2）在3.9小时内卸完货才不会受台风影响
【解析】试题分析：(1)、过B作BD⊥AC于D，根据Rt△ABD的性质得出BD的长度，从而得出答案；(2)、以B为圆心，200海里为半径画圆交AC于E，F两点，连接BE，BF，根据垂径定理得出DE的长度，从而求出AE的长度，最后求出时间．
试题解析：(1)、如图所示，过B作BD⊥AC于D，在Rt△ABD中，
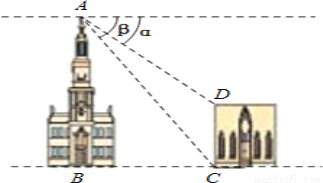
B... 如图，两建筑物的水平距离BC为18m，从A点测得D点的俯角α为30°，测得C点的俯角β为60°．则建筑物CD的高度为 m（结果不作近似计算）．
【解析】
试题分析：过点D作DE⊥AB于点E，
则四边形BCDE是矩形，
根据题意得：∠ACB=β=60°，∠ADE=α=30°，BC=18m，
∴DE=BC=18m，CD=BE，
在Rt△ABC中，AB=BC•tan∠ACB=18×tan60°=18（m），
在Rt△ADE中，AE=DE•tan∠ADE=18×tan30°=6（m），
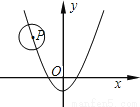
∴DC=BE=AB... 如图，已知⊙P的半径为2，圆心P在抛物线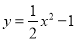
上运动，当⊙P与x轴相切时，圆心P的坐标为_____________
（，2）或（，2）
【解析】试题分析：依题意，可设P（x，2）或P（x，﹣2）．
①当P的坐标是（x，2）时，将其代入y=x2﹣1，得
2=x2﹣1，
解得x=±，
此时P（，2）或（﹣，2）；
②当P的坐标是（x，﹣2）时，将其代入y=x2﹣1，得
﹣2=x2﹣1，即﹣1=x2
无解．
综上所述，符合条件的点P的坐标是（，2）或（﹣，2） 二次函数y＝x2＋bx＋c的图象经过点(4，3)，(3，0)．
(1)求b、c的值；
(2)求出该二次函数图象的顶点坐标和对称轴；
(3)画出二次函数y＝x2＋bx＋c的图象．
(1)b＝－4，c＝3；(2) (2，－1)，x＝2；(3)画图见解析.
【解析】试题分析：（1）把已知点的坐标代入解析式，然后解关于b、c的二元一次方程组即可得解；
（2）把函数解析式转化为顶点式形式，然后即可写出顶点坐标与对称轴解析式；
（3）采用列表、描点法画出图象即可．
试题解析：（1）∵二次函数y=x2+bx+c的图象经过点（4，3），（3，0），
∴
解得
...