题目内容
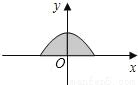
如图所示是二次函数y=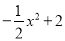
的图象在x轴上方的一部分，对于这段图象与x轴所围成的阴影部分的面积，你认为可能的值是（ ）
A. 4 B.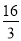 
C. 2π D. 8
B
【解析】函数与y轴交于（0，2）点，与x轴交于（-2，0）和（2，0）两点，则三点构成的三角形面积S1=4，则以半径为2的半圆的面积为S2=π××22=2π，则阴影部分的面积S有：4＜S＜2π．因为选项A、C、D均不在S取值范围内．故选 B
练习册系列答案
同步练习河南大学出版社系列答案
同步练习西南大学出版社系列答案
补充习题江苏系列答案
相关题目
在△ABC中，AB =AC，∠A=80°，则∠B=__________.
50°
【解析】∵AB=AC，
∴根据轴对称的性质，将线段BC对折重合后，点A在折痕上，
∴线段AB、AC关于折痕轴对称，
设折痕与BC交点为D，
则△ABD、△ACD关于直线AD轴对称，
∴∠B=∠C =(180°－∠A)÷2=（180°－80°)÷2=50°.
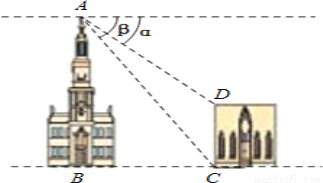
故答案为：50°. 如图，两建筑物的水平距离BC为18m，从A点测得D点的俯角α为30°，测得C点的俯角β为60°．则建筑物CD的高度为 m（结果不作近似计算）．
【解析】
试题分析：过点D作DE⊥AB于点E，
则四边形BCDE是矩形，
根据题意得：∠ACB=β=60°，∠ADE=α=30°，BC=18m，
∴DE=BC=18m，CD=BE，
在Rt△ABC中，AB=BC•tan∠ACB=18×tan60°=18（m），
在Rt△ADE中，AE=DE•tan∠ADE=18×tan30°=6（m），
∴DC=BE=AB... 如图，已知⊙P的半径为2，圆心P在抛物线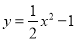
上运动，当⊙P与x轴相切时，圆心P的坐标为_____________
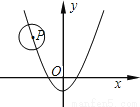
（，2）或（，2）
【解析】试题分析：依题意，可设P（x，2）或P（x，﹣2）．
①当P的坐标是（x，2）时，将其代入y=x2﹣1，得
2=x2﹣1，
解得x=±，
此时P（，2）或（﹣，2）；
②当P的坐标是（x，﹣2）时，将其代入y=x2﹣1，得
﹣2=x2﹣1，即﹣1=x2
无解．
综上所述，符合条件的点P的坐标是（，2）或（﹣，2） 将进货单价为70元的某种商品按零售价100元一个售出时，每天能卖出20个，若这种商品的零售价每降价1元，其日销量就增加1个，为了获取每日最大利润，则应降价（ ）
A. 5元 B. 10元 C. 15元 D. 20元
A
【解析】设应降价x元，总利润为y元，根据题意可得：
，
化简、配方得：
，
∴当时，y最大=625，
∴ B、C、D错误，选A. 二次函数y=ax2＋bx＋c(a≠0)的图象如图所示，根据图象解答下列问题．
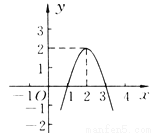
(1)写出方程ax2＋bx＋c＝0的两个根；
(2)写出不等式ax2＋bx＋c＞0的解集；
(3)写出y随x的增大而减小的自变量x的取值范围；
(4)若方程ax2＋bx＋c＝k有两个不相等的实数根，求k的取值范围．
（1）x＝1或x＝3是方程ax2＋bx＋c＝0的两个根；（2）l＜x＜3；（3）当x＞2时，y随x的增大而减小；（4）k＜2．
【解析】试题分析：（1）观察图形可以看出抛物线与x轴交于（1，0）和（3，0），即可解题
（2）根据抛物线y=ax2+bx+c，求得y＞0的x取值范围即可解题；
（3）图中可以看出抛物线对称轴，即可解题；
（3）易求得抛物线解析式，根据方程△＞0即... 已知函数y=kx2-7x-7的图象和x轴有交点，则k的取值范围是__________
【解析】【解析】
分两种情况讨论：①若k=0，则y=-7x-7是一次函数，与x轴有交点；
②若k≠0，则函数y=kx2-7x-7是二次函数．∵二次函数y=kx2﹣7x﹣7的图象和x轴有交点，∴，∴k≥且k≠0．
综上所述：k≥．故答案为：k≥． 二次函数y＝x2＋bx＋c的图象经过点(4，3)，(3，0)．
(1)求b、c的值；
(2)求出该二次函数图象的顶点坐标和对称轴；
(3)画出二次函数y＝x2＋bx＋c的图象．
(1)b＝－4，c＝3；(2) (2，－1)，x＝2；(3)画图见解析.
【解析】试题分析：（1）把已知点的坐标代入解析式，然后解关于b、c的二元一次方程组即可得解；
（2）把函数解析式转化为顶点式形式，然后即可写出顶点坐标与对称轴解析式；
（3）采用列表、描点法画出图象即可．
试题解析：（1）∵二次函数y=x2+bx+c的图象经过点（4，3），（3，0），
∴
解得
... 如图，斜面AC的坡度（CD与AD的比）为1:2，AC=
米，坡顶有一旗杆BC，旗杆顶端B点与A点有一条彩带相连，若AB=10米，则旗杆BC的高度为（ ）
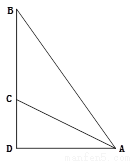
A. 5米 B. 6米 C. 8米 D.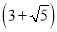 
米
A
【解析】试题分析：根据CD：AD=1:2，AC=3米可得：CD=3米，AD=6米，根据AB=10米，∠D=90°可得：BD==8米，则BC=BD－CD=8－3=5米.