��Ŀ����
��ABC�У�AB=AC����A=36�㣬��ABC�͡�ACB��ƽ����BE��CD���ڵ�F�����е���������( ��
A. 7�� B. 8�� C. 9�� D. 10��
 B
���������ߵ�������������������ȣ�
��ֻҪ���жϳ�����������Ⱦ����ˣ�
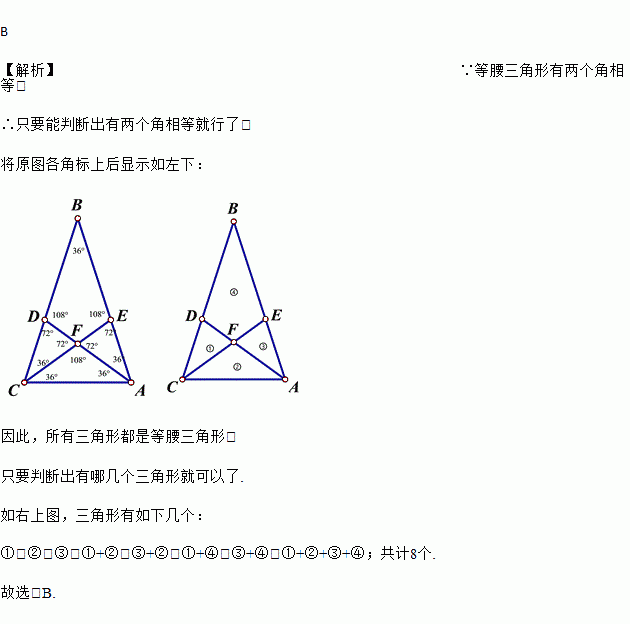
��ԭͼ���DZ��Ϻ���ʾ�����£�
��ˣ����������ζ��ǵ��������Σ�
ֻҪ�жϳ����ļ��������ξͿ�����.
������ͼ�������������¼�����
�٣��ڣ��ۣ���+�ڣ���+�ڣ���+�ܣ���+�ܣ���+��+��+�ܣ�����8��.
��ѡ��B.
B
���������ߵ�������������������ȣ�
��ֻҪ���жϳ�����������Ⱦ����ˣ�
��ԭͼ���DZ��Ϻ���ʾ�����£�
��ˣ����������ζ��ǵ��������Σ�
ֻҪ�жϳ����ļ��������ξͿ�����.
������ͼ�������������¼�����
�٣��ڣ��ۣ���+�ڣ���+�ڣ���+�ܣ���+�ܣ���+��+��+�ܣ�����8��.
��ѡ��B.
 53������ϵ�д�
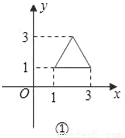
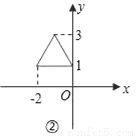
53������ϵ�д�����ͼ������е���������ȣ����е������η����ı仯�ǣ�������
A. ����ƽ��3����λ B. ����ƽ��2����λ
C. ����ƽ��3����λ D. ����ƽ��1����λ
 A
����������������
��ͼ�ٵ�ͼ�ڣ��㣨1��1��ƽ�Ƶ��㣨��2��1����
�㣨3��1��ƽ�Ƶ��㣨0��1������������ƽ��3����λ��
��ͼ��ƽ�ƹ���Ϊ������ƽ��3����λ��
��ѡA��
A
����������������
��ͼ�ٵ�ͼ�ڣ��㣨1��1��ƽ�Ƶ��㣨��2��1����
�㣨3��1��ƽ�Ƶ��㣨0��1������������ƽ��3����λ��
��ͼ��ƽ�ƹ���Ϊ������ƽ��3����λ��
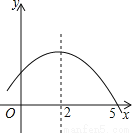
��ѡA�� ��ͼ�Ƕ��κ���y=ax2+bx+c�IJ���ͼ����ͼ���֪����ʽax2+bx+c��0�Ľ⼯�ǣ�������
A. -1��x��5 B. x��5 C. x��-1��x��5 D. x��-1��x��5
 D
����������ͼ��֪�������ߵĶԳ���Ϊֱ��x=2����x���һ����������Ϊ��5��0����
�ຯ��ͼ����x�����һ��������Ϊ��-1��0����
��ax2+bx+c��0�Ľ⼯��x��-1��x��5��
��ѡC.
D
����������ͼ��֪�������ߵĶԳ���Ϊֱ��x=2����x���һ����������Ϊ��5��0����
�ຯ��ͼ����x�����һ��������Ϊ��-1��0����
��ax2+bx+c��0�Ľ⼯��x��-1��x��5��
��ѡC. ���и�ʽ�����ҵı����У�����ʽ�ֽ���ǣ� ��.
A. x��a-b��=ax-bx B. x2-1+y2=��x-1����x+1��+y2
C. y2-1=��y+1����y-1�� D. ax+bx+c=x��a+b��+c
 C
��������A. ����ʽ�ij˷�����A����
B. û��һ������ʽת���ɼ�����ʽ������B����
C. ��һ������ʽת���ɼ�����ʽ������C��ȷ��
D. û��һ������ʽת���ɼ�����ʽ������D����
��ѡ��C.
C
��������A. ����ʽ�ij˷�����A����
B. û��һ������ʽת���ɼ�����ʽ������B����
C. ��һ������ʽת���ɼ�����ʽ������C��ȷ��
D. û��һ������ʽת���ɼ�����ʽ������D����
��ѡ��C. �ڡ�ABC�У�AB =AC����A=80�㣬���B=__________.
 50��
����������AB=AC��
�������ԳƵ����ʣ����߶�BC�����غϺ�A���ۺ��ϣ�
���߶�AB��AC�����ۺ���Գƣ�
���ۺ���BC����ΪD��
���ABD����ACD����ֱ��AD��Գƣ�
���B=��C =(180�㣭��A)��2=��180�㣭80��)��2=50��.
�ʴ�Ϊ��50��.
50��
����������AB=AC��
�������ԳƵ����ʣ����߶�BC�����غϺ�A���ۺ��ϣ�
���߶�AB��AC�����ۺ���Գƣ�
���ۺ���BC����ΪD��
���ABD����ACD����ֱ��AD��Գƣ�
���B=��C =(180�㣭��A)��2=��180�㣭80��)��2=50��.
�ʴ�Ϊ��50��. ����ͼ���У�������Գ�ͼ�ε��ǣ� ��
A. �������ڽ���ȵ������� B. ��һ���ڽ�Ϊ45���ֱ��������
C. �������ڽǷֱ�Ϊ50���80��������� D. �������ڽǷֱ�Ϊ55���65���������
 D
��������A.�������ڽ���ȵ��������ǵ��������Σ���������������Գ�ͼ�Σ�
B.��һ���ڽ�Ϊ45�ȵ�ֱ���������ǵ���ֱ�������Σ�Ҳ�ǵ��������Σ�����Գ�ͼ�Σ�C.�������ڽǷֱ�Ϊ50�Ⱥ�80�ȵ������Σ�����������50�ȣ����ǵ��������Σ�����Գ�ͼ�Σ�
D.�������ڽǷֱ�Ϊ55�Ⱥ�65�ȵ�������,���ǵ��������Σ�������Գ�ͼ��.
��ѡ��D.
D
��������A.�������ڽ���ȵ��������ǵ��������Σ���������������Գ�ͼ�Σ�
B.��һ���ڽ�Ϊ45�ȵ�ֱ���������ǵ���ֱ�������Σ�Ҳ�ǵ��������Σ�����Գ�ͼ�Σ�C.�������ڽǷֱ�Ϊ50�Ⱥ�80�ȵ������Σ�����������50�ȣ����ǵ��������Σ�����Գ�ͼ�Σ�
D.�������ڽǷֱ�Ϊ55�Ⱥ�65�ȵ�������,���ǵ��������Σ�������Գ�ͼ��.
��ѡ��D. �����ĸ�ͼ���У�������Գ�ͼ�ε��ǣ� ��
A. ��һ���ڽ�Ϊ45�ȵ�ֱ�������� B. ��һ���ڽ�Ϊ60�ȵĵ���������
C. ��һ���ڽ�Ϊ30�ȵ�ֱ�������� D. �����ڽǷֱ�Ϊ36�Ⱥ�72�ȵ�������
 C
��������A.��һ���ڽ�Ϊ45�ȵ�ֱ�������Σ������ڽǷֱ���45�㡢90�㡢45�㣬�ǵ��������Σ�����Գ�ͼ�Σ�
B.��һ���ڽ�Ϊ60��ĵ��������Σ������Ƕ����ֱ�Ϊ60�㡢60�㡢60�㣬�ǵȱ������Σ�����Գ�ͼ�Σ�����C����һ���ڽ�Ϊ30�ȵ�ֱ�������Σ������Ƕ����ֱ�Ϊ30�㡢90�㡢60�㣬���ǵ��������Σ�������Գ�ͼ�Σ�
D.�����ڽǷֱ�Ϊ36�Ⱥ�72�ȵ������Σ�������...
C
��������A.��һ���ڽ�Ϊ45�ȵ�ֱ�������Σ������ڽǷֱ���45�㡢90�㡢45�㣬�ǵ��������Σ�����Գ�ͼ�Σ�
B.��һ���ڽ�Ϊ60��ĵ��������Σ������Ƕ����ֱ�Ϊ60�㡢60�㡢60�㣬�ǵȱ������Σ�����Գ�ͼ�Σ�����C����һ���ڽ�Ϊ30�ȵ�ֱ�������Σ������Ƕ����ֱ�Ϊ30�㡢90�㡢60�㣬���ǵ��������Σ�������Գ�ͼ�Σ�
D.�����ڽǷֱ�Ϊ36�Ⱥ�72�ȵ������Σ�������... ��ͼ��ʾ��ij������20���ʱ���ٶȽ�һ����Ҫ������A���������������B������16Сʱ������������ж������ʱ�ӵ�������֪ͨ��һ̨����������40���ʱ���ٶ���A����ƫ��60���AC�����ƶ�����̨������200�����Բ������(�����߽�)�����ܵ�Ӱ�죺
(1)B���Ƿ���ܵ�̨���Ӱ��?��˵�����ɣ�
(2)Ϊ����ж�������ܵ�̨��Ӱ�죬������ԱӦ�ڶ���Сʱ��ж�����?(��ȷ��0.1Сʱ�� 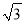 ��1.732)
��1.732)
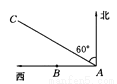
 ��1��B�����ܵ�̨���Ӱ�죨2����3.9Сʱ��ж����Ų�����̨��Ӱ��
�����������������(1)����B��BD��AC��D������Rt��ABD�����ʵó�BD�ij��ȣ��Ӷ��ó��𰸣�(2)����BΪԲ�ģ�200����Ϊ�뾶��Բ��AC��E��F���㣬����BE��BF�����ݴ��������ó�DE�ij��ȣ��Ӷ����AE�ij��ȣ�������ʱ�䣮
���������(1)����ͼ��ʾ����B��BD��AC��D����Rt��ABD�У�
B...
��1��B�����ܵ�̨���Ӱ�죨2����3.9Сʱ��ж����Ų�����̨��Ӱ��
�����������������(1)����B��BD��AC��D������Rt��ABD�����ʵó�BD�ij��ȣ��Ӷ��ó��𰸣�(2)����BΪԲ�ģ�200����Ϊ�뾶��Բ��AC��E��F���㣬����BE��BF�����ݴ��������ó�DE�ij��ȣ��Ӷ����AE�ij��ȣ�������ʱ�䣮
���������(1)����ͼ��ʾ����B��BD��AC��D����Rt��ABD�У�
B... ���κ���y=ax2��bx��c(a��0)��ͼ����ͼ��ʾ������ͼ�����������⣮
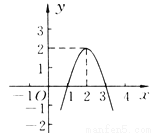
(1)�����ax2��bx��c��0����������
(2)д������ʽax2��bx��c��0�Ľ⼯��
(3)д��y��x���������С���Ա���x��ȡֵ��Χ��
(4)������ax2��bx��c��k����������ȵ�ʵ��������k��ȡֵ��Χ��
 ��1��x��1��x��3�Ƿ���ax2��bx��c��0������������2��l��x��3����3����x��2ʱ��y��x���������С����4��k��2��
�������������������1���۲�ͼ�ο��Կ�����������x�ύ�ڣ�1��0���ͣ�3��0�������ɽ���
��2������������y=ax2+bx+c�����y��0��xȡֵ��Χ���ɽ��⣻
��3��ͼ�п��Կ��������߶Գ��ᣬ���ɽ��⣻
��3������������߽���ʽ�����ݷ��̡���0��...
��1��x��1��x��3�Ƿ���ax2��bx��c��0������������2��l��x��3����3����x��2ʱ��y��x���������С����4��k��2��
�������������������1���۲�ͼ�ο��Կ�����������x�ύ�ڣ�1��0���ͣ�3��0�������ɽ���
��2������������y=ax2+bx+c�����y��0��xȡֵ��Χ���ɽ��⣻
��3��ͼ�п��Կ��������߶Գ��ᣬ���ɽ��⣻
��3������������߽���ʽ�����ݷ��̡���0��...