题目内容
15.关于x的一元二次方程:x2-4x-m2=0有两个实数根x1、x2,则m2($\frac{1}{{x}_{1}}+\frac{1}{{x}_{2}}$)=( )| A. | $\frac{{m}^{4}}{4}$ | B. | $-\frac{{m}^{4}}{4}$ | C. | 4 | D. | -4 |
分析 根据所给一元二次方程,写出韦达定理,代入所求式子化简.
解答 解:∵x2-4x-m2=0有两个实数根x1、x2,
∴$\left\{\begin{array}{l}{{x}_{1}+{x}_{2}=4}\\{{x}_{1}{x}_{2}=-{m}^{2}}\end{array}\right.$,
∴则m2($\frac{1}{{x}_{1}}+\frac{1}{{x}_{2}}$)=${m}^{2}•\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$=${m}^{2}•\frac{4}{-{m}^{2}}$=-4.
故答案选D.
点评 本题主要考查一元二次方程根与系数的关系,属基础题,熟练掌握韦达定理是解题关键.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
5.2-(-1)=( )
| A. | 1 | B. | 2 | C. | -3 | D. | 3 |
7.数学老师将全班分成7个小组开展小组合作学习,采用随机抽签确定一个小组进行展示活动,则第3个小组被抽到的概率是( )
| A. | $\frac{1}{7}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{21}$ | D. | $\frac{1}{10}$ |
5. 如图,在4×4的正方形方格图形中,小正方形的顶点称为格点,△ABC的顶点都在格点上,则图中∠ABC的余弦值是( )
如图,在4×4的正方形方格图形中,小正方形的顶点称为格点,△ABC的顶点都在格点上,则图中∠ABC的余弦值是( )
 如图,在4×4的正方形方格图形中,小正方形的顶点称为格点,△ABC的顶点都在格点上,则图中∠ABC的余弦值是( )
如图,在4×4的正方形方格图形中,小正方形的顶点称为格点,△ABC的顶点都在格点上,则图中∠ABC的余弦值是( )| A. | 2 | B. | $\frac{{2\sqrt{5}}}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{5}}}{5}$ |
 测量计算是日常生活中常见的问题,如图,建筑物BC的屋顶有一根旗杆AB,从地面上D点处观测旗杆顶点A的仰角为50°,观测旗杆底部B点的仰角为45°,(可用的参考数据:sin50°≈0.8,tan50°≈1.2)
测量计算是日常生活中常见的问题,如图,建筑物BC的屋顶有一根旗杆AB,从地面上D点处观测旗杆顶点A的仰角为50°,观测旗杆底部B点的仰角为45°,(可用的参考数据:sin50°≈0.8,tan50°≈1.2)
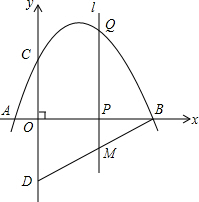 如图,抛物线y=-$\frac{1}{2}{x}^{2}+\frac{3}{2}x+2$与x轴交于点A,点B,与y轴交于点C,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.
如图,抛物线y=-$\frac{1}{2}{x}^{2}+\frac{3}{2}x+2$与x轴交于点A,点B,与y轴交于点C,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.