题目内容
(1)|-
|+(-1)2014-2cos45°+
.
(2)先化简,再求值:
÷(
-
),其中x=
+1,y=
-1.
| 2 |
| 16 |
(2)先化简,再求值:
| x2+y2-2xy |
| x-y |
| x |
| y |
| y |
| x |
| 2 |
| 2 |
考点:分式的化简求值,实数的运算,特殊角的三角函数值
专题:计算题
分析:(1)原式第一项利用绝对值的代数意义化简,第二项利用乘方的意义化简,第三项利用特殊角的三角函数值计算,最后一项利用平方根定义化简,计算即可得到结果;
(2)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,将x与y的值代入计算即可求出值.
(2)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,将x与y的值代入计算即可求出值.
解答:解:(1)原式=
+1-2×
+4=5;
(2)原式=
÷
=
•
=
,
当x=
+1,y=
-1时,xy=1,x+y=2
,
则原式=
=
.
| 2 |
| ||
| 2 |
(2)原式=
| (x-y)2 |
| x-y |
| (x+y)(x-y) |
| xy |
| (x-y)2 |
| x-y |
| xy |
| (x+y)(x-y) |
| xy |
| x+y |
当x=
| 2 |
| 2 |
| 2 |
则原式=
| 1 | ||
2
|
| ||
| 4 |
点评:此题考查了分式的化简求值,以及实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
一个正数的两个平方根分别为a-7和2a+1,则a是( )
| A、-1 | B、-2 | C、1 | D、2 |
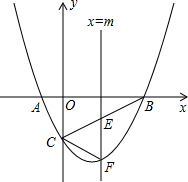 如图,抛物线y=ax2+bx-2与x轴交于A、B两点,与y轴交于点C,已知A(-1,0),且tan∠ABC=
如图,抛物线y=ax2+bx-2与x轴交于A、B两点,与y轴交于点C,已知A(-1,0),且tan∠ABC= 如图,在矩形ABCD中,点E是CD的中点,点F是边AD上一点,连结FE并廷长交BC的延长线于点G,连接BF、BE.且BE⊥FG;
如图,在矩形ABCD中,点E是CD的中点,点F是边AD上一点,连结FE并廷长交BC的延长线于点G,连接BF、BE.且BE⊥FG; 如图,△ABC中,AB=4cm,AC=6cm,∠A=60°,求BC的长.
如图,△ABC中,AB=4cm,AC=6cm,∠A=60°,求BC的长. 如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(-1,2),B(-3,4),C(-2,9).
如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(-1,2),B(-3,4),C(-2,9). 已知,在Rt△OAB中,∠OAB=90°,∠BOA=30°,OA=2
已知,在Rt△OAB中,∠OAB=90°,∠BOA=30°,OA=2