题目内容
 如图,在矩形ABCD中,点E是CD的中点,点F是边AD上一点,连结FE并廷长交BC的延长线于点G,连接BF、BE.且BE⊥FG;
如图,在矩形ABCD中,点E是CD的中点,点F是边AD上一点,连结FE并廷长交BC的延长线于点G,连接BF、BE.且BE⊥FG;(1)求证:BF=BG.
(2)若tan∠BFG=
| 3 |
| 3 |
考点:相似三角形的判定与性质,勾股定理,矩形的性质
专题:
分析:(1)证明△EDF≌△ECG,则EF=EG,即可证得BE是FG的中垂线,根据线段的中垂线的性质即可证得;
(2)根据∠BFG=∠G,在直角△ECG中,根据正切的定义即可求得边长的比值,然后根据面积,即可求得CG的长,然后根据EC是直角△BGE的斜边上的高线,利用射影定理即可求得BC,即可求得AD的长.
(2)根据∠BFG=∠G,在直角△ECG中,根据正切的定义即可求得边长的比值,然后根据面积,即可求得CG的长,然后根据EC是直角△BGE的斜边上的高线,利用射影定理即可求得BC,即可求得AD的长.
解答:(1)证明:∵四边形ABCD是矩形,
∴∠D=∠DCG=90°.
在△EDF和△ECG中,
∴△EDF≌△ECG
∴EF=EG
∵BE⊥FG
∴BE是FG的中垂线,
∴BF=BG;
(2)解:∵BF=BG
∴∠BFG=∠G
∴tan∠BFG=tan∠G=
设CG=x,CE=
x,
则S△CGE=
x2=6
,
解得:x=2
∴CG=2
,CE=6
由射影定理得:EC2=BC•CG,
∴BC=6
∴AD=6
∴∠D=∠DCG=90°.
在△EDF和△ECG中,
|
∴△EDF≌△ECG
∴EF=EG
∵BE⊥FG
∴BE是FG的中垂线,
∴BF=BG;
(2)解:∵BF=BG
∴∠BFG=∠G
∴tan∠BFG=tan∠G=
| 3 |
设CG=x,CE=
| 3 |
则S△CGE=
| ||
| 2 |
| 3 |
解得:x=2
| 3 |
∴CG=2
| 3 |
由射影定理得:EC2=BC•CG,
∴BC=6
| 3 |
∴AD=6
| 3 |
点评:本题考查了正方形的性质以及全等三角形的判定与性质,射影定理的应用,正确证明BE是FG的中垂线是关键.

练习册系列答案
相关题目
在直线y=-
x+3上到x轴的距离等于2的点的坐标为( )
| 1 |
| 2 |
| A、(2,2) |
| B、(10,-2) |
| C、(2,2)和(10,-2) |
| D、(2,-2)和(10,2) |
 如图,在△ABC中,CE⊥AB于E,DF⊥AB于F,AC∥ED,且∠EDF=∠BDF.求证:CE是∠ACB的平分线.
如图,在△ABC中,CE⊥AB于E,DF⊥AB于F,AC∥ED,且∠EDF=∠BDF.求证:CE是∠ACB的平分线.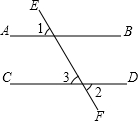 填空:已知:如图,∠1=∠2,求证:AB∥CD
填空:已知:如图,∠1=∠2,求证:AB∥CD 如图,一次函数y=kx+2与反比例函数y=
如图,一次函数y=kx+2与反比例函数y=