题目内容
 已知,在Rt△OAB中,∠OAB=90°,∠BOA=30°,OA=2
已知,在Rt△OAB中,∠OAB=90°,∠BOA=30°,OA=2| 3 |
(1)求A、B、C三点的坐标;
(2)求经过点O、C、A三点的抛物线的解析式,并求抛物线的对称轴与线段OB交点D的坐标;
(3)在线段OD上有一点P,过P作直线PM∥CD,交抛物线于点M,若四边形PDCM是平行四边形,求P点的坐标.
考点:二次函数综合题
专题:
分析:(1)通过解直角三角形求得AO、AB的值,从而得出A、B的坐标,然后根据折叠的性质可知:∠COB=30°,OC=OA=2
,进而得出∠COH=60°,OH=
,CH=3,所以C点的坐标为(
,3);
(2)根据待定系数法求得抛物线的解析式和直线OB的解析式,由两个解析式构成方程组,解这个方程组即可求得交点D的坐标.
(3)根据抛物线的解析式和直线BO的解析式设出P、M的坐标,根据平行四边形的性质:对应边相等列出方程,解方程即可.
| 3 |
| 3 |
| 3 |
(2)根据待定系数法求得抛物线的解析式和直线OB的解析式,由两个解析式构成方程组,解这个方程组即可求得交点D的坐标.
(3)根据抛物线的解析式和直线BO的解析式设出P、M的坐标,根据平行四边形的性质:对应边相等列出方程,解方程即可.
解答: 解:(1)∵在RT△OAB中,∠OAB=90°,∠BOA=30°,OA=2
解:(1)∵在RT△OAB中,∠OAB=90°,∠BOA=30°,OA=2
,
∴OB=
=4,AB=2,
∵AO=2
,AB=2,
∴A(2
,0),B(2
,2),
过点C作CH⊥x轴于H,
有折叠的性质可知:∠COB=30°,OC=OA=2
,
∴∠COH=60°,OH=
,CH=3,
∴C点的坐标为(
,3);
(2)∵O点的坐标为(0,0),
∴抛物线的解析式为y=ax2+bx,(a≠0),
∵经过点C(
,3)、A(2
,0),
∴
解得:
,
∴此抛物线的函数关系式为:y=-x2+2
x,
∵AO=2
,AB=2,
∴B(2
,2),
∴设直线BO的解析式为:y=kx,
则2=2
k,
解得:k=
∴直线BO为:y=
x,
∵抛物线y=-x2+2
x的对称轴为x=-
=
,
∴代入y=
x得:y=1,
∴抛物线的对称轴与线段OB交点D的坐标(
,1).
(3)如图,由(2)可知:抛物线的对称轴为x=
,C(
,3)
∴C点就是抛物线的顶点,
∵四边形PDCM是平行四边形,
∴PM∥CD∥y轴,PM=CD,
∵C(
,3),D(
,1).
∴CD=2,
设P(m,
m),则M(m,-m2+2
m),
∴PM=-m2+2
m-
m,
∴-m2+2
m-
m=2,
解得:m=
(舍去),m=
,
∴P(
,
).
 解:(1)∵在RT△OAB中,∠OAB=90°,∠BOA=30°,OA=2
解:(1)∵在RT△OAB中,∠OAB=90°,∠BOA=30°,OA=2| 3 |
∴OB=
| cos30° |
| AO |
∵AO=2
| 3 |
∴A(2
| 3 |
| 3 |
过点C作CH⊥x轴于H,
有折叠的性质可知:∠COB=30°,OC=OA=2
| 3 |
∴∠COH=60°,OH=
| 3 |
∴C点的坐标为(
| 3 |
(2)∵O点的坐标为(0,0),
∴抛物线的解析式为y=ax2+bx,(a≠0),
∵经过点C(
| 3 |
| 3 |
∴
|
|
∴此抛物线的函数关系式为:y=-x2+2
| 3 |
∵AO=2
| 3 |
∴B(2
| 3 |
∴设直线BO的解析式为:y=kx,
则2=2
| 3 |
解得:k=
| ||
| 3 |
∴直线BO为:y=
| ||
| 3 |
∵抛物线y=-x2+2
| 3 |
2
| ||
| -2 |
| 3 |
∴代入y=
| ||
| 3 |
∴抛物线的对称轴与线段OB交点D的坐标(
| 3 |
(3)如图,由(2)可知:抛物线的对称轴为x=
| 3 |
| 3 |
∴C点就是抛物线的顶点,
∵四边形PDCM是平行四边形,
∴PM∥CD∥y轴,PM=CD,
∵C(
| 3 |
| 3 |
∴CD=2,
设P(m,
| ||
| 3 |
| 3 |
∴PM=-m2+2
| 3 |
| ||
| 3 |
∴-m2+2
| 3 |
| ||
| 3 |
解得:m=
| 3 |
2
| ||
| 3 |
∴P(
2
| ||
| 3 |
| 2 |
| 3 |
点评:本题考查了直角三角形的三角函数的求值,待定系数法求解析式,函数图象的交点坐标,抛物线的对称轴和顶点坐标,平行四边形的性质等;

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
 如图,在△ABC中,CE⊥AB于E,DF⊥AB于F,AC∥ED,且∠EDF=∠BDF.求证:CE是∠ACB的平分线.
如图,在△ABC中,CE⊥AB于E,DF⊥AB于F,AC∥ED,且∠EDF=∠BDF.求证:CE是∠ACB的平分线.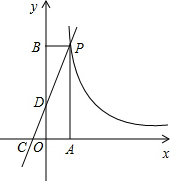 如图,一次函数y=kx+2与反比例函数y=
如图,一次函数y=kx+2与反比例函数y= 如图,矩形ABCD中,AD=a,AB=b,依次连结它的各边中点得到第一个四边形E1F1G1H1,再依次连结四边形E1F1G1H1的各边中点得到第二个四边形E2F2G2H2,按此方法继续下去,得到的第n个四边形EnFnGnHn的面积等于
如图,矩形ABCD中,AD=a,AB=b,依次连结它的各边中点得到第一个四边形E1F1G1H1,再依次连结四边形E1F1G1H1的各边中点得到第二个四边形E2F2G2H2,按此方法继续下去,得到的第n个四边形EnFnGnHn的面积等于