题目内容
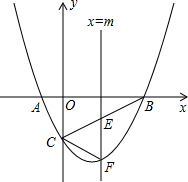 如图,抛物线y=ax2+bx-2与x轴交于A、B两点,与y轴交于点C,已知A(-1,0),且tan∠ABC=
如图,抛物线y=ax2+bx-2与x轴交于A、B两点,与y轴交于点C,已知A(-1,0),且tan∠ABC=| 1 |
| 2 |
(1)求抛物线的解析式和直线BC的解析式;
(2)若△CEF为等腰三角形,求m的值;
(3)点P为y轴左侧抛物线上的一点,过点P作PM⊥BC交直线BC于点M,连接PB,若∠BPM=∠ABC,求P点的坐标.
考点:二次函数综合题
专题:
分析:(1)根据题意易求点A、B的坐标,把它们的坐标代入抛物线解析式,利用方程求得系数a、b的值;把点B、C的坐标代入直线方程,利用待定系数法求得直线BC的方程;
(2)此题需要分类讨论:分别以点C、E、F为顶点的等腰三角形.由等腰三角形的性质和两点间的距离公式来求m的值;
(3)根据题意易证:△PHM∽△MRB,由该相似三角形的对应边成比例和锐角三角函数的定义推知PH、HM、PQ间的数量关系,然后根据二次函数图象上点的坐标特征来求点P的坐标即可.
(2)此题需要分类讨论:分别以点C、E、F为顶点的等腰三角形.由等腰三角形的性质和两点间的距离公式来求m的值;
(3)根据题意易证:△PHM∽△MRB,由该相似三角形的对应边成比例和锐角三角函数的定义推知PH、HM、PQ间的数量关系,然后根据二次函数图象上点的坐标特征来求点P的坐标即可.
解答:解:(1)由题意得:C(0,-2).
∵tan∠ABC=
=
=
,
∴OB=4,
∴B(4,0).将A(-1,0),B(4,0)代入y=ax2+bx-2,得
,
解得
.
则抛物线的解析式为:y=
x2-
x-2.
设直线BC的解析式为:y=kx+n(k≠0).
把B(4,0),C(0,-2)代入得:
,
解得
,
故直线BC为:y=
x-2;
(2)∵由(1)知,抛物线的解析式为:y=
x2-
x-2.直线BC为:y=
x-2.
∴E(m,
m-2),F(m,
m2-
m-2),(0<m<4).
则CE2=m2+(
m)2=
m2,CF2=m2+(
m2-
m)2=
m4-
m3+
m2,EF2=(
m2-2m)2=
m4-2m3+4m2.
①若以C为顶点,则CE2=CF2,即
m2═
m4-
m3+
m2,
解得 m1=2,m2=4(不合题意,舍去);
②若以点E为顶点时,CE2=EF2,即
m2=
m4-2m3+4m2.
解得 m3=4-
,m4=4+
(不合题意,舍去);
③若以点F为顶点时,CF2=EF2,即
m4-
m3+
m2=
m4-2m3+4m2.
解得 m5=
.
综上所述,符合条件的m值为:2或4-
或
;
(3)如图:过点M作与x轴平行的直线,分别作P点、B点与该直线的垂线交于点H、R,连接PH、BR、HR
易证△PHM∽△MRB,
∴
=
=
.
又∵x轴∥HR,
∴∠ABC=∠BMR,
∴tan∠BMR=tan∠ABC=
=
.
令BR=a,MR=2a.
又∵∠BPM=∠ABC,
∴tan∠BPM=tan∠ABC=
=
,
∴
=
=
,
∴HP=4a,HM=2a,PQ=3a,
∴HR=4a,
∴P(4-4a,3a).
又∵点P在抛物线上,把P(4-4a,3a)代入y=
x2-
x-2,得
(4-4a)2-
(4-4a)-2=3a,
整理,得8a2-13a=0,
解得 a1=0(舍去),a2=
.
∴P(-
,
).
∵tan∠ABC=
| CO |
| BO |
| 2 |
| BO |
| 1 |
| 2 |
∴OB=4,
∴B(4,0).将A(-1,0),B(4,0)代入y=ax2+bx-2,得
|
解得
|
则抛物线的解析式为:y=
| 1 |
| 2 |
| 3 |
| 2 |
设直线BC的解析式为:y=kx+n(k≠0).
把B(4,0),C(0,-2)代入得:
|
解得
|
故直线BC为:y=
| 1 |
| 2 |
(2)∵由(1)知,抛物线的解析式为:y=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
∴E(m,
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
则CE2=m2+(
| 1 |
| 2 |
| 5 |
| 4 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 4 |
| 3 |
| 2 |
| 13 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
①若以C为顶点,则CE2=CF2,即
| 5 |
| 4 |
| 1 |
| 4 |
| 3 |
| 2 |
| 13 |
| 4 |
解得 m1=2,m2=4(不合题意,舍去);
②若以点E为顶点时,CE2=EF2,即
| 5 |
| 4 |
| 1 |
| 4 |
解得 m3=4-
| 5 |
| 5 |
③若以点F为顶点时,CF2=EF2,即
| 1 |
| 4 |
| 3 |
| 2 |
| 13 |
| 4 |
| 1 |
| 4 |
解得 m5=
| 3 |
| 2 |

综上所述,符合条件的m值为:2或4-
| 5 |
| 3 |
| 2 |
(3)如图:过点M作与x轴平行的直线,分别作P点、B点与该直线的垂线交于点H、R,连接PH、BR、HR
易证△PHM∽△MRB,
∴
| PH |
| MR |
| HM |
| BR |
| PM |
| MB |
又∵x轴∥HR,
∴∠ABC=∠BMR,
∴tan∠BMR=tan∠ABC=
| BR |
| MR |
| 1 |
| 2 |
令BR=a,MR=2a.
又∵∠BPM=∠ABC,
∴tan∠BPM=tan∠ABC=
| BM |
| PM |
| 1 |
| 2 |
∴
| PH |
| MR |
| HM |
| BR |
| 1 |
| 2 |
∴HP=4a,HM=2a,PQ=3a,
∴HR=4a,
∴P(4-4a,3a).
又∵点P在抛物线上,把P(4-4a,3a)代入y=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
整理,得8a2-13a=0,
解得 a1=0(舍去),a2=
| 13 |
| 8 |
∴P(-
| 5 |
| 2 |
| 39 |
| 8 |
点评:本题考查了二次函数综合题型.其中涉及到了待定系数法求二次函数、一次函数解析式,二次函数图象上点的坐标特征,相似三角形的判定与性质以及等腰三角形的性质.注意,对于动点问题,需要分类讨论.

练习册系列答案
相关题目
 如图,直线AB与直线CD相交于点O,OE⊥AB,垂足为O,∠EOD=30°,则∠BOC=( )
如图,直线AB与直线CD相交于点O,OE⊥AB,垂足为O,∠EOD=30°,则∠BOC=( )| A、150° | B、140° |
| C、130° | D、120° |
点P(-6,4)在哪个象限?( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
 如图,在△ABC中,CE⊥AB于E,DF⊥AB于F,AC∥ED,且∠EDF=∠BDF.求证:CE是∠ACB的平分线.
如图,在△ABC中,CE⊥AB于E,DF⊥AB于F,AC∥ED,且∠EDF=∠BDF.求证:CE是∠ACB的平分线. 如图所示,?ABCD的对角线AC、BD相交于点O,BD=12cm,点E在线段BO上从点B开始以1cm/s的速度运动,点F在线段OD上从O点开始以2cm/s的速度运动.若点E、F同时运动,且当点F运动到D点时,点E、F同时停止运动,设运动时间为ts,当t为何值时,四边形AECF是平行四边形?
如图所示,?ABCD的对角线AC、BD相交于点O,BD=12cm,点E在线段BO上从点B开始以1cm/s的速度运动,点F在线段OD上从O点开始以2cm/s的速度运动.若点E、F同时运动,且当点F运动到D点时,点E、F同时停止运动,设运动时间为ts,当t为何值时,四边形AECF是平行四边形?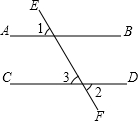 填空:已知:如图,∠1=∠2,求证:AB∥CD
填空:已知:如图,∠1=∠2,求证:AB∥CD