题目内容
已知⊙O的半径为6cm,弦AB=6cm,弦AC=6
cm,则∠CAB等于 度.
| 3 |
考点:垂径定理,特殊角的三角函数值
专题:分类讨论
分析:分当B和C分别位于A的两侧和当B和C位于A的同侧两种情况,则∠CAB=∠CAO+∠OAB或∠CAB=∠OAB-∠OAC,根据垂径定理和三角函数即可求解.
解答: 解:当B和C分别位于A的两侧时,如图1.
解:当B和C分别位于A的两侧时,如图1.
连接OA、OB,作OD⊥AC于点D.
∵OA=OB=AB=6cm,
∴△OAB是等边三角形,
∴∠OAB=60°,
∵OD⊥AC于点D,
∴AD=
AC=
×6
=3
,
∴在直角△ODA中,cos∠CAO=
=
=
,
∴∠CAO=30°,
∴∠CAB=∠CAO+∠OAB=30°+60°=90°;
当B和C位于A的同侧,如图2.
∠CAB=∠OAB-∠OAC=60°-30°=30°.
故答案是:90或30.
 解:当B和C分别位于A的两侧时,如图1.
解:当B和C分别位于A的两侧时,如图1.连接OA、OB,作OD⊥AC于点D.
∵OA=OB=AB=6cm,
∴△OAB是等边三角形,
∴∠OAB=60°,
∵OD⊥AC于点D,
∴AD=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
∴在直角△ODA中,cos∠CAO=
| AD |
| OA |
3
| ||
| 6 |
| ||
| 2 |
∴∠CAO=30°,
∴∠CAB=∠CAO+∠OAB=30°+60°=90°;
当B和C位于A的同侧,如图2.
∠CAB=∠OAB-∠OAC=60°-30°=30°.
故答案是:90或30.
点评:本题考查了垂径定理和三角函数,注意到分当B和C分别位于A的两侧和同侧两种情况进行讨论是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,⊙O是△ABC的外接圆,且AB=AC=5,BC=8,则⊙O的半径为
如图,⊙O是△ABC的外接圆,且AB=AC=5,BC=8,则⊙O的半径为 如图,公园内有一颗景观树,AB的影子请好落在地图BC和地图CD上,经测量CD=4m,BC=10m,已知该坡面CD与地面成30°角,且此时测得2m的竹竿的影子是1m,求这颗景观树的高度.
如图,公园内有一颗景观树,AB的影子请好落在地图BC和地图CD上,经测量CD=4m,BC=10m,已知该坡面CD与地面成30°角,且此时测得2m的竹竿的影子是1m,求这颗景观树的高度.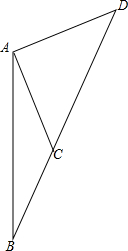 如图,距沿海某城市A的正南方向240千米B处有一台风中心,该台风中心现正以20千米/小时速度沿北偏东30°方向直线移动,当台风到达C处时,对A城市造成影响,一直到离开D处时,影响消失.已知AC=AD=200千米,问该台风影响该城市持续的时间有多长?
如图,距沿海某城市A的正南方向240千米B处有一台风中心,该台风中心现正以20千米/小时速度沿北偏东30°方向直线移动,当台风到达C处时,对A城市造成影响,一直到离开D处时,影响消失.已知AC=AD=200千米,问该台风影响该城市持续的时间有多长?