题目内容
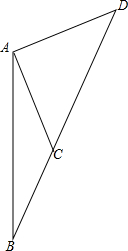 如图,距沿海某城市A的正南方向240千米B处有一台风中心,该台风中心现正以20千米/小时速度沿北偏东30°方向直线移动,当台风到达C处时,对A城市造成影响,一直到离开D处时,影响消失.已知AC=AD=200千米,问该台风影响该城市持续的时间有多长?
如图,距沿海某城市A的正南方向240千米B处有一台风中心,该台风中心现正以20千米/小时速度沿北偏东30°方向直线移动,当台风到达C处时,对A城市造成影响,一直到离开D处时,影响消失.已知AC=AD=200千米,问该台风影响该城市持续的时间有多长?考点:解直角三角形的应用-方向角问题
专题:
分析:过点A作AE⊥CD于点E,根据等腰三角形三线合一的性质得出CD=2CE,再解直角△ABE,得出AE=
AB=120千米,在直角△ACE中利用勾股定理求出CE,得到CD,然后根据时间=路程÷速度即可求解.
| 1 |
| 2 |
解答: 解:如图,过点A作AE⊥CD于点E,
解:如图,过点A作AE⊥CD于点E,
∵AC=AD,
∴CD=2CE.
在直角△ABE中,∵∠AEB=90°,∠B=30°,AB=240千米,
∴AE=
AB=120千米.
在直角△ACE中,∵∠AEC=90°,AC=200千米,AE=120千米,
∴CE=
=160千米,
∴CD=2CE=320千米,
∵台风中心的速度为每小时20千米,
∴该台风影响该城市持续的时间为320÷20=16(小时).
 解:如图,过点A作AE⊥CD于点E,
解:如图,过点A作AE⊥CD于点E,∵AC=AD,
∴CD=2CE.
在直角△ABE中,∵∠AEB=90°,∠B=30°,AB=240千米,
∴AE=
| 1 |
| 2 |
在直角△ACE中,∵∠AEC=90°,AC=200千米,AE=120千米,
∴CE=
| AC2-AE2 |
∴CD=2CE=320千米,
∵台风中心的速度为每小时20千米,
∴该台风影响该城市持续的时间为320÷20=16(小时).
点评:本题考查了解直角三角形的应用-方向角问题,等腰三角形的性质,勾股定理以及含30°角的直角三角形的性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,四边形ABCD中,过点D作DE⊥AB,作DF⊥BC,垂足分别为点E、F,∠EDF=60°,若BE=14,BF=2,求平行四边形ABCD的周长和面积.
如图,四边形ABCD中,过点D作DE⊥AB,作DF⊥BC,垂足分别为点E、F,∠EDF=60°,若BE=14,BF=2,求平行四边形ABCD的周长和面积. 求证:同弧或等弧所对的圆周角都相等.(求证:∠ADB=∠ACB)
求证:同弧或等弧所对的圆周角都相等.(求证:∠ADB=∠ACB) 如图,已知直角△ABC的两条边AC、AB的长分别为2
如图,已知直角△ABC的两条边AC、AB的长分别为2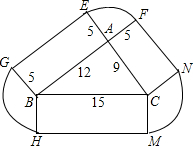 如图所示,一个房屋地基呈三角形状.三角形的边长分别为9米、12米、15米,花园由距地基边界5米之内的土地构成,问房屋连同花园共占地多少平方米?(精确到1平方米)
如图所示,一个房屋地基呈三角形状.三角形的边长分别为9米、12米、15米,花园由距地基边界5米之内的土地构成,问房屋连同花园共占地多少平方米?(精确到1平方米)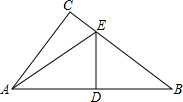 如图,在△ABC,∠C=90°,DE垂直平分斜边AB,分别交AB、BC于D、E.若∠CAE=∠B+40°,求∠AEB的度数.
如图,在△ABC,∠C=90°,DE垂直平分斜边AB,分别交AB、BC于D、E.若∠CAE=∠B+40°,求∠AEB的度数.