题目内容
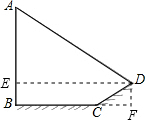
 如图,公园内有一颗景观树,AB的影子请好落在地图BC和地图CD上,经测量CD=4m,BC=10m,已知该坡面CD与地面成30°角,且此时测得2m的竹竿的影子是1m,求这颗景观树的高度.
如图,公园内有一颗景观树,AB的影子请好落在地图BC和地图CD上,经测量CD=4m,BC=10m,已知该坡面CD与地面成30°角,且此时测得2m的竹竿的影子是1m,求这颗景观树的高度.考点:解直角三角形的应用-坡度坡角问题,相似三角形的应用
专题:
分析:作DE⊥AB于点E,DF⊥BC于点F,在Rt△CDF中,利用含30°角的直角三角形的性质可得DF长,也就是BE的长,还可以求得CF的长,也就求得了BF的长,也就是ED的长;易得AE与影长DE构成的三角形和竹杆与影长构成的三角形相似,利用相似三角形的对应边成比例可得AB的长.
解答:解:作DE⊥AB于点E,DF⊥BC于点F.
在Rt△CDF中,∵CD=4m,∠DCF=30°,
∴DF=
CD=2m,CF=
DF=2
m,
∴BE=DF=2m,
∴ED=BF=BC+CF=(10+2
)m.
∵同一时刻的光线是平行的,水平线是平行的,
∴光线与水平线的夹角相等,
又∵标竿与影长构成的角为直角,AE与ED构成的角为直角,
∴AE与影长DE构成的三角形和竹竿与影长构成的三角形相似,
∴
=
,
解得AE=(20+4
)m,
∴AB=AE+BE=(22+4
)m.
答:AB的长为(22+4
)m.

在Rt△CDF中,∵CD=4m,∠DCF=30°,
∴DF=
| 1 |
| 2 |
| 3 |
| 3 |
∴BE=DF=2m,
∴ED=BF=BC+CF=(10+2
| 3 |
∵同一时刻的光线是平行的,水平线是平行的,
∴光线与水平线的夹角相等,
又∵标竿与影长构成的角为直角,AE与ED构成的角为直角,
∴AE与影长DE构成的三角形和竹竿与影长构成的三角形相似,
∴
| AE |
| DE |
| 2 |
| 1 |
解得AE=(20+4
| 3 |
∴AB=AE+BE=(22+4
| 3 |
答:AB的长为(22+4
| 3 |
点评:本题考查了解直角三角形的应用-坡度坡角问题以及相似三角形的应用,用到的知识点为:两角对应相等的两三角形相似;相似三角形的对应边成比例.作出两条辅助线构造出2个直角三角形是解决本题的突破点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,OE为∠AOD的平分线,∠COD=
如图,OE为∠AOD的平分线,∠COD=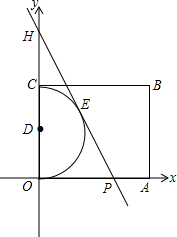 如图,在直角坐标系中,半圆直径为OC,半圆圆心D的坐标为(0,2),四边形OABC是矩形,∠OPH=60°.半圆D的切线PH分别与x轴和y轴相交于点P与点H,切点为点E.
如图,在直角坐标系中,半圆直径为OC,半圆圆心D的坐标为(0,2),四边形OABC是矩形,∠OPH=60°.半圆D的切线PH分别与x轴和y轴相交于点P与点H,切点为点E. 求证:同弧或等弧所对的圆周角都相等.(求证:∠ADB=∠ACB)
求证:同弧或等弧所对的圆周角都相等.(求证:∠ADB=∠ACB)