题目内容
10. 如图,正方形的边长为2,边OA,OC分别在x轴与y轴上,反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象经过正方形的中心D.
如图,正方形的边长为2,边OA,OC分别在x轴与y轴上,反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象经过正方形的中心D.(1)直接写出点D的坐标;
(2)求反比例函数的解析式.
分析 (1)根据正方形的性质即可求得D的坐标;
(2)根据待定系数法即可求得反比例函数的解析式.
解答 解:(1)∵正方形的边长为2,边OA,OC分别在x轴与y轴上,
∴A(2,0),C(0,2),B(2,2),
∵点D是正方形的中心,
∴D(1,1);
(2)设反比例函数的解析式为y=$\frac{k}{x}$,
且该函数图象过点D(1,1),
∴$\frac{k}{1}$=1,
∴k=1,
∴反比例函数的解析式为y=$\frac{1}{x}$.
点评 本题考查了正方形的性质和待定系数法求反比例函数的解析式,熟练掌握待定系数法是解题的关键.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
1.某商店代销一批季节性服装,每套代销成本40元,第一个月每套销售定价为52元时,可售出180套;应市场变化需上调第一个月的销售价,预计销售定价每增加1元,销售量将减少10套.
(1)若设第二个月的销售定价每套增加x元,填写表格:
(2)若商店预计要在第二个月的销售中获利2000元,则第二个月销售定价每套多少元?
(3)若要使第二个月利润达到最大,应定价为多少?此时第二个月的最大利润是多少?
(1)若设第二个月的销售定价每套增加x元,填写表格:
| 时间 | 第一个月 | 第二个月 |
| 销售定价(元) | 52 | 52+x |
| 销售量(套) | 180 | 180-10x |
(3)若要使第二个月利润达到最大,应定价为多少?此时第二个月的最大利润是多少?
19.若“!”是一种运算符号,且1!=1,2!=2×1,3!=3×2×1,4!=4×3×2×1,…,则计算$\frac{2015!}{2014!}$正确的是( )
| A. | 2015 | B. | 2014 | C. | $\frac{2015}{2014}$ | D. | 2015×2014 |
20.一组数据1,-1,0,-1,1的方差是( )
| A. | 0 | B. | 0.64 | C. | 1 | D. | 0.8 |
 如图,在数轴上点A表示1,现将点A沿x轴做如下移动:第一次点A向左移动3个单位长度到达点A1,第二次将点A1向右移动6个单位长度到达点A2,第三次将点A2向左移动9个单位长度到达点A3,按照这种移动规律移动下去.第n次移动到点An,则点A2015表示的数是-3023.
如图,在数轴上点A表示1,现将点A沿x轴做如下移动:第一次点A向左移动3个单位长度到达点A1,第二次将点A1向右移动6个单位长度到达点A2,第三次将点A2向左移动9个单位长度到达点A3,按照这种移动规律移动下去.第n次移动到点An,则点A2015表示的数是-3023.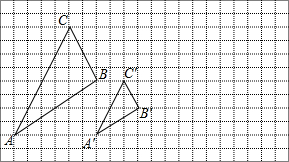 如图,△ABC 与△A′B′C′是以点O为位似中心的位似图形,它们的顶点都在正方形网格的格点上.
如图,△ABC 与△A′B′C′是以点O为位似中心的位似图形,它们的顶点都在正方形网格的格点上.