题目内容
15．
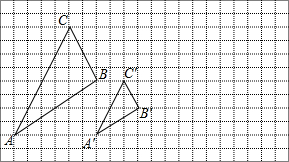如图，△ABC 与△A′B′C′是以点O为位似中心的位似图形，它们的顶点都在正方形网格的格点上．（1）画出位似中心O；
（2）△ABC与△A′B′C′的相似比为2：1，面积比为4：1．
分析 （1）根据位似的性质，延长AA′、BB′、CC′，则它们的交点即为位似中心O；
（2）根据位似的性质得到AB：A′B′=OA：OA′=2：1，则△ABC与△A′B′C′的相似比为2：1，然后根据相似三角形的性质得到它们面积的比．
解答 解：（1）如图，点O为位似中心；
（2）因为AB：A′B′=OA：OA′=12：6=2：1，
所以△ABC与△A′B′C′的相似比为2：1，面积比为4：1．
故答案为2：1； 4：1．
点评 本题考查了作图-位似变换：先确定位似中心；再分别连接并延长位似中心和能代表原图的关键点；然后根据位似比，确定能代表所作的位似图形的关键点；最后顺次连接上述各点，得到放大或缩小的图形．
练习册系列答案
相关题目
5．下列成语故事中所描述的事件为必然发生事件的是（ ）
| A． | 水中捞月 | B． | 瓮中捉鳖 | C． | 拔苗助长 | D． | 守株待兔 |
如图，正方形的边长为2，边OA，OC分别在x轴与y轴上，反比例函数y=$\frac{k}{x}$（k为常数，k≠0）的图象经过正方形的中心D．
已知抛物线y=ax2+bx+4在坐标系中的位置如图所示，它与x，y轴的交点分别为A（-1，0），B，P是其对称轴x=1上的动点，根据图中提供的信息，得出以下结论：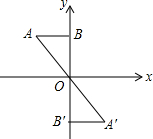
如图，平面直角坐标系内点A（-2，3），B（0，3），将△OAB绕点O顺时针旋转180°，得到△OA′B′，则点A′的坐标是（2，-3）．
如图，在△ABC中，∠ABC和∠ACB的平分线相交于点O，若∠A=42°．