题目内容
16.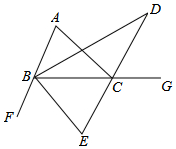 如图,∠CBF、∠ACG是△ABC的外角,∠ACG的平分线所在的直线分别与∠ABC、∠CBF的平分线BD、BE交于点D、E.
如图,∠CBF、∠ACG是△ABC的外角,∠ACG的平分线所在的直线分别与∠ABC、∠CBF的平分线BD、BE交于点D、E.(1)求∠DBE的度数;
(2)若∠A=70°,求∠D的度数;
(3)若∠A=a,则∠D=$\frac{1}{2}$α,∠E=90°-$\frac{1}{2}$α(用含a的式子表示)
分析 (1)根据角平分线的定义得到∠DBC=$\frac{1}{2}∠$ABC,∠CBE=$\frac{1}{2}∠$CBF,于是得到结论;
(2)由角平分线的定义得到∠DCG=$\frac{1}{2}∠$ACG,∠DBC=$\frac{1}{2}∠$ABC,然后根据三角形的内角和即可得到结论;
(3)由(2)知∠D=$\frac{1}{2}∠$A,根据三角形的内角和得到∠E=90°-$\frac{1}{2}$α.
解答 解:(1)∵BD平分∠ABC,BE平分∠CBF,
∴∠DBC=$\frac{1}{2}∠$ABC,∠CBE=$\frac{1}{2}∠$CBF,
∴∠DBC+∠CBE=$\frac{1}{2}$(∠ABC+∠CBF)=90°,
∴∠DBE=90°;
(2)∵CD平分∠ACG,BD平分∠ABC,
∴∠DCG=$\frac{1}{2}∠$ACG,∠DBC=$\frac{1}{2}∠$ABC,
∵∠ACD=∠A+∠ABC,
∴2∠DCG=∠ACF=∠A+∠ABC=∠A+2∠DBC,
∵∠DCG=∠D+∠DBC,
∴2∠DCG=2∠D+2∠DBC,
∴∠A+2∠DBC=2∠D+2∠DBC,
∴∠D=$\frac{1}{2}∠$A=35°;
(3)由(2)知∠D=$\frac{1}{2}∠$A,
∵∠A=α,
∴∠D=$\frac{1}{2}α$,
∵∠DBE=90°,
∴∠E=90°-$\frac{1}{2}$α.
故答案为:$\frac{1}{2}α$,90°-$\frac{1}{2}α$.
点评 本题考查三角形内角和定理,角平分线的定义,外角性质,熟练掌握外角性质是解题的关键.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
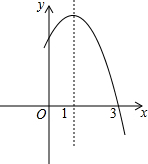 已知二次函数y=-x2+2x+m的部分图象如图所示.
已知二次函数y=-x2+2x+m的部分图象如图所示.