题目内容
4.计算(1)$\sqrt{18}$-$\sqrt{72}$+$\sqrt{50}$
(2)($\sqrt{7}$+$\sqrt{3}$)($\sqrt{7}$-$\sqrt{3}$)-$\sqrt{16}$
(3)$\frac{\sqrt{18}+\sqrt{2}}{\sqrt{2}}$-3
(4)$\root{3}{8}$+$\sqrt{0}$-$\sqrt{\frac{1}{4}}$
(5)$\left\{\begin{array}{l}{3m+2n=16}\\{3m-n=1}\end{array}\right.$
(6)$\left\{\begin{array}{l}{x+3y=7}\\{y-x=1}\end{array}\right.$
(7)$\left\{\begin{array}{l}{y=x+6\\;}\\{2x+3y=8}\end{array}\right.$
(8)$\left\{\begin{array}{l}{2x+3y=-19}\\{x+5y=1}\end{array}\right.$.
分析 (1)原式化简合并即可得到结果;
(2)原式利用平方差公式,以及算术平方根定义计算即可得到结果;
(3)原式利用二次根式乘除法则计算即可得到结果;
(4)原式利用立方根、平方根定义计算即可得到结果;
(5)方程组利用加减消元法求出解即可;
(6)方程组利用加减消元法求出解即可;
(7)方程组利用代入消元法求出解即可;
(8)方程组利用加减消元法求出解即可.
解答 解:(1)原式=3$\sqrt{2}$-6$\sqrt{2}$+5$\sqrt{2}$=2$\sqrt{2}$;
(2)原式=7-3-4=0;
(3)原式=3+1-3=1;
(4)原式=2+0-$\frac{1}{2}$=1$\frac{1}{2}$;
(5)$\left\{\begin{array}{l}{3m+2n=16①}\\{3m-n=1②}\end{array}\right.$,
①-②得:3n=15,即n=5,
把n=5代入②得:m=2,
则方程组的解为$\left\{\begin{array}{l}{m=2}\\{n=5}\end{array}\right.$;
(6)$\left\{\begin{array}{l}{x+3y=7①}\\{x-y=-1②}\end{array}\right.$,
①-②得:4y=8,即y=2,
把y=2代入②得:x=1,
则方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$;
(7)$\left\{\begin{array}{l}{y=x+6①}\\{2x+3y=8②}\end{array}\right.$,
把①代入②得:2x+3x+18=8,即x=-2,
把x=-2代入①得:y=4,
则方程组的解为$\left\{\begin{array}{l}{x=-2}\\{y=4}\end{array}\right.$;
(8)$\left\{\begin{array}{l}{2x+3y=-19①}\\{x+5y=1②}\end{array}\right.$,
②×2-①得:7y=21,即y=3,
把y=3代入②得:x=-14,
则方程组的解为$\left\{\begin{array}{l}{x=-14}\\{y=3}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案 如图,在热气球上A处测得一栋大楼顶部B的俯角为23°,测得这栋大楼底部C的俯角为45°.已知热气球A处距地面的高度为180m,求这栋大楼的高度(精确到1m).(参考数据:sin23°=0.39,cos23°=0.92,tan23°=0.42)
如图,在热气球上A处测得一栋大楼顶部B的俯角为23°,测得这栋大楼底部C的俯角为45°.已知热气球A处距地面的高度为180m,求这栋大楼的高度(精确到1m).(参考数据:sin23°=0.39,cos23°=0.92,tan23°=0.42) 如图,A,E,C,F在同一条直线上,AB=FD,BC=DE,AE=FC.△ABC与△FDE全等吗?说明理由.
如图,A,E,C,F在同一条直线上,AB=FD,BC=DE,AE=FC.△ABC与△FDE全等吗?说明理由.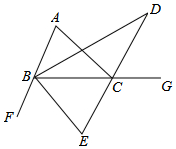 如图,∠CBF、∠ACG是△ABC的外角,∠ACG的平分线所在的直线分别与∠ABC、∠CBF的平分线BD、BE交于点D、E.
如图,∠CBF、∠ACG是△ABC的外角,∠ACG的平分线所在的直线分别与∠ABC、∠CBF的平分线BD、BE交于点D、E.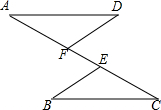 如图,已知AE=CF,AD=BC,DF=BE.
如图,已知AE=CF,AD=BC,DF=BE.