题目内容
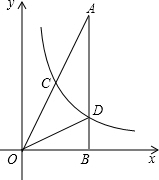 如图,在△AOB中,∠ABO=90°,OB=4,AB=8,反比例函数y=
如图,在△AOB中,∠ABO=90°,OB=4,AB=8,反比例函数y=| k |
| x |
(1)求反比例函数解析式;
(2)求点C的坐标.
考点:反比例函数与一次函数的交点问题
专题:代数几何综合题
分析:(1)根据反比例函数k的几何意义得到
×k=4,解得k=8,所以反比例函数解析式为y=
;
(2)先确定A点坐标,再利用待定系数法求出直线OA的解析式为y=2x,然后解方程组
即可得到C点坐标.
| 1 |
| 2 |
| 8 |
| x |
(2)先确定A点坐标,再利用待定系数法求出直线OA的解析式为y=2x,然后解方程组
|
解答:解:(1)∵∠ABO=90°,S△BOD=4,
∴
×k=4,解得k=8,
∴反比例函数解析式为y=
;
(2)∵∠ABO=90°,OB=4,AB=8,
∴A点坐标为(4,8),
设直线OA的解析式为y=kx,
把A(4,8)代入得4k=8,解得k=2,
∴直线OA的解析式为y=2x,
解方程组
得
或
,
∵C在第一象限,
∴C点坐标为(2,4).
∴
| 1 |
| 2 |
∴反比例函数解析式为y=
| 8 |
| x |

(2)∵∠ABO=90°,OB=4,AB=8,
∴A点坐标为(4,8),
设直线OA的解析式为y=kx,
把A(4,8)代入得4k=8,解得k=2,
∴直线OA的解析式为y=2x,
解方程组
|
|
|
∵C在第一象限,
∴C点坐标为(2,4).
点评:本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数解析式.也考查了待定系数法求函数解析式.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
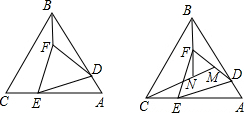 如图,等边△ABC中,D、E分别在AB、AC边上,且CE=2AD,将线段DE绕点D顺时针旋转60°得到线段DF,连接EF、BF;
如图,等边△ABC中,D、E分别在AB、AC边上,且CE=2AD,将线段DE绕点D顺时针旋转60°得到线段DF,连接EF、BF; 已知一次函数的图象经过点(1,1)和点(-1,-3).
已知一次函数的图象经过点(1,1)和点(-1,-3).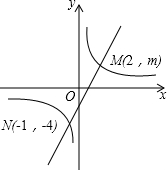 如图,一次函数y=ax+b的图象与反比例函数y=
如图,一次函数y=ax+b的图象与反比例函数y=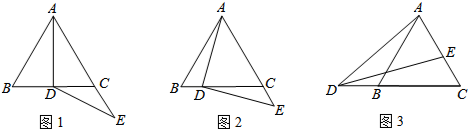
 如图,点P为∠BAC内的一点,点E、F分别是点P关于AB、AC的对称点,若EF=2013cm.则△QPK的周长是
如图,点P为∠BAC内的一点,点E、F分别是点P关于AB、AC的对称点,若EF=2013cm.则△QPK的周长是