题目内容
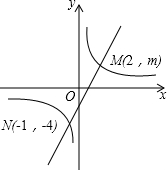 如图,一次函数y=ax+b的图象与反比例函数y=
如图,一次函数y=ax+b的图象与反比例函数y=| k |
| x |
(1)利用图中条件,求反比例函数和一次函数的解析式;
(2)根据图象写出使反比例函数的值大于一次函数的值的x的取值范围.
考点:反比例函数与一次函数的交点问题
专题:计算题
分析:(1)先把N点坐标代入y=
求出k得反比例函数解析式为y=
,在利用反比例函数解析式确定M点的坐标为(2,2),然后利用待定系数法求一次函数解析式;
(2)观察函数图象得到当x>-1或0<x<2时,反比例函数图象都在以此函数图象上方,即反比例函数的值大于一次函数的值.
| k |
| x |
| 4 |
| x |
(2)观察函数图象得到当x>-1或0<x<2时,反比例函数图象都在以此函数图象上方,即反比例函数的值大于一次函数的值.
解答:解:(1)把N(-1,-4)代入y=
得k=-1×(-4)=4,
所以反比例函数解析式为y=
;
把M(2,m)代入y=
得2m=4,解得m=2,
则M点的坐标为(2,2),
把M(2,2),N(-1,-4)代入y=ax+b得
,解得
,
所以一次函数解析式为y=2x-2;
(2)x>-1或0<x<2.
| k |
| x |
所以反比例函数解析式为y=
| 4 |
| x |
把M(2,m)代入y=
| 4 |
| x |
则M点的坐标为(2,2),
把M(2,2),N(-1,-4)代入y=ax+b得
|
|
所以一次函数解析式为y=2x-2;
(2)x>-1或0<x<2.
点评:本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数解析式.也考查了待定系数法求函数解析式以及观察函数图象的能力.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
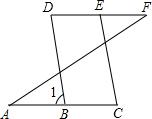 如图,已知:∠A=∠F,∠C=∠D,求证:BD∥EC,下面是不完整的说明过程,请将过程及其依据补充完整.
如图,已知:∠A=∠F,∠C=∠D,求证:BD∥EC,下面是不完整的说明过程,请将过程及其依据补充完整.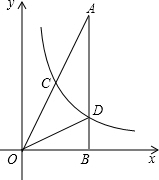 如图,在△AOB中,∠ABO=90°,OB=4,AB=8,反比例函数y=
如图,在△AOB中,∠ABO=90°,OB=4,AB=8,反比例函数y= 已知:如图,BE=CF,AB=DE,AC=DF,求证:△ABC≌△DEF.
已知:如图,BE=CF,AB=DE,AC=DF,求证:△ABC≌△DEF.