题目内容
分解因式:
(1)3x2+5xy-2y2+x+9y-4;
(2)a3+1;
(3)4x4-13x2+9;
(4)x2+x-(a2-a).
(1)3x2+5xy-2y2+x+9y-4;
(2)a3+1;
(3)4x4-13x2+9;
(4)x2+x-(a2-a).
考点:因式分解
专题:
分析:(1)先将3x2+5xy-2y2进行因式分解,再变形为(3x-y)(x+2y)-(3x-y)+4(x+2y-1),进一步即可求解;
(2)根据立方和公式即可求解;
(3)先因式分解法进行因式分解,再根据平方差公式进行因式分解;
(4)先变形为(x2-a2)+(x-a),再根据平方差公式和提取公因式法进行因式分解.
(2)根据立方和公式即可求解;
(3)先因式分解法进行因式分解,再根据平方差公式进行因式分解;
(4)先变形为(x2-a2)+(x-a),再根据平方差公式和提取公因式法进行因式分解.
解答:解:(1)3x2+5xy-2y2+x+9y-4
=(3x-y)(x+2y)+x+9y-4
=(3x-y)(x+2y)-(3x-y)+4x+8y-4
=(3x-y)(x+2y-1)+4(x+2y-1)
=(3x-y+4)(x+2y-1);
(2)a3+1=(a+1)(a2-a+1)
(3)4x4-13x2+9
=(4x2-9)(x-1)
=(2x+3)(2x-3)(x+1)(x-1);
(4)x2+x-(a2-a)
=(x2-a2)+(x-a)
=(x+a)(x-a)+(x-a)
=(x-a)(x+a+1).
=(3x-y)(x+2y)+x+9y-4
=(3x-y)(x+2y)-(3x-y)+4x+8y-4
=(3x-y)(x+2y-1)+4(x+2y-1)
=(3x-y+4)(x+2y-1);
(2)a3+1=(a+1)(a2-a+1)
(3)4x4-13x2+9
=(4x2-9)(x-1)
=(2x+3)(2x-3)(x+1)(x-1);
(4)x2+x-(a2-a)
=(x2-a2)+(x-a)
=(x+a)(x-a)+(x-a)
=(x-a)(x+a+1).
点评:本题考查了因式分解,一个多项式有公因式首先提取公因式,然后再用其他方法进行因式分解,同时因式分解要彻底,直到不能分解为止.

练习册系列答案
相关题目
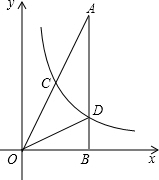 如图,在△AOB中,∠ABO=90°,OB=4,AB=8,反比例函数y=
如图,在△AOB中,∠ABO=90°,OB=4,AB=8,反比例函数y=
 如图,直线AB、CD被直线EF所截,则∠1的内错角是
如图,直线AB、CD被直线EF所截,则∠1的内错角是