Question

11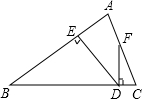．如图所示，△ABC中，AB=BC，DE⊥AB于点E，DF⊥BC于点D，交AC于F．
（1）若∠AFD=155°，求∠EDF的度数；
（2）若点F是AC的中点，猜想∠CFD与∠B的数量关系，并证明．

Answer 1

分析 （1）根据已知条件得到∠DFC=25°，根据垂直的定义得到FDC=∠AED=90°，根据周角的定义即可得到结论；
（2）连接BF，根据等腰三角形的性质得到BF⊥AC，∠ABF=∠CBF=$\frac{1}{2}$∠ABC，根据余角的性质得到∠CFD=∠CBF，于是得到结论．

解答 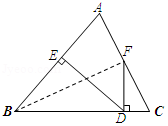解：（1）∵∠AFD=155°，
∴∠DFC=25°，
∵DF⊥BC，DE⊥AB，
∴∠FDC=∠AED=90°，
在Rt△EDC中，
∴∠C=90°-25°=65°，
∵AB=BC，
∴∠C=∠A=65°，
∴∠EDF=360°-65°-155°-90°=50°；
（2）∠CFD=$\frac{1}{2}$∠ABC，
连接BF，
∵AB=BC，且点F是AC的中点，
∴BF⊥AC，∠ABF=∠CBF=$\frac{1}{2}$∠ABC，
∴∠CFD+∠BFD=90°，
∠CBF+∠BFD=90°，
∴∠CFD=∠CBF，
∴∠CFD=$\frac{1}{2}$∠ABC．

点评 本题考查了等腰三角形的性质，直角三角形的性质，正确的作出辅助线是解题的关键．