题目内容
19.数学老师在黑板上抄写了一道题目:“当a=2,b=-2时,求多项式3a3b3-$\frac{1}{2}$a2b+b-(4a3b3-$\frac{1}{4}$a2b-b2)+(a3b3+$\frac{1}{4}$a2b)-2b2+3的值”,甲同学做题时把a=2抄错成a=-2,乙同学没抄错题,但他们得出的结果恰好一样,这是怎么回事儿呢?分析 原式去括号合并得到最简结果,即可作出判断.
解答 解:原式=3a3b3-$\frac{1}{2}$a2b+b-4a3b3+$\frac{1}{4}$a2b+b2+a3b3+$\frac{1}{4}$a2b-2b2+3=b-b2+3,
结果与a的值无关,故做题时把a=2抄错成a=-2,乙同学没抄错题,但他们得出的结果恰好一样.
点评 此题考查了整式的加减-化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
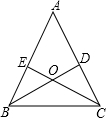 已知:如图,锐角△ABC的两条高BD、CE相交于点O,且OB=OC.
已知:如图,锐角△ABC的两条高BD、CE相交于点O,且OB=OC.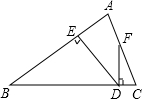 如图所示,△ABC中,AB=BC,DE⊥AB于点E,DF⊥BC于点D,交AC于F.
如图所示,△ABC中,AB=BC,DE⊥AB于点E,DF⊥BC于点D,交AC于F. 如图是由六块积木搭成,这几块积木都是相同的正方体,请画出这个图形的三视图.
如图是由六块积木搭成,这几块积木都是相同的正方体,请画出这个图形的三视图.