题目内容
1.若抛物线y=ax2+k的图象经过点(0,-2),(1,-1),(1)试确定这个二次函数的解析式;
(2)写出图象的开口方向、对称轴和顶点坐标,图象与x轴的交点坐标.
分析 (1)利用二次函数图象上点的坐标性质将已知点代入求出答案;
(2)由抛物线的解析式容易得出开口方向、对称轴以及顶点坐标;求出y=0时x的值,即可得出图象与x轴的交点坐标.
解答 解:∵抛物线y=ax2+k经过点(0,-2),(1,-1),
∴∴$\left\{\begin{array}{l}{k=-2}\\{a+k=-1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=1}\\{k=-2}\end{array}\right.$,
∴这个二次函数的解析式为:y=x2-2;
(2)∵a=1>0,
∴抛物线的开口向上,
对称轴为y轴,顶点坐标为(0,-2);
当y=0时,x2-2=0,解得:x=±$\sqrt{2}$,
∴抛物线与x轴的交点坐标为(-$\sqrt{2}$,0),($\sqrt{2}$,0).
点评 此题主要考查了二次函数解析式的求法、抛物线与x轴的交点坐标;用待定系数法求出抛物线的解析式是解决问题的关键.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
6.下列计算正确的是( )
| A. | (am)n=am+n | B. | 2a+a=3a2 | C. | (a2b)3=a6b3 | D. | a2•a3=a6 |
7.据统计,宁波全市2014年实现地区生产总值7602.51亿元,同比增长7.6%.其中7602.51亿元用科学记数法可表示为( )
| A. | 7.60251×1013元 | B. | 7.60251×1012元 | C. | 7.60251×1011元 | D. | 8.972031×1010元 |

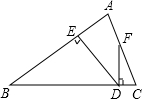 如图所示,△ABC中,AB=BC,DE⊥AB于点E,DF⊥BC于点D,交AC于F.
如图所示,△ABC中,AB=BC,DE⊥AB于点E,DF⊥BC于点D,交AC于F.