题目内容
1. 如图,二次函数y=ax2+bx-3的图象与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C,该抛物线的顶点为M.
如图,二次函数y=ax2+bx-3的图象与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C,该抛物线的顶点为M.(1)求该抛物线的解析式;
(2)判断△BCM的形状,并说明理由.
分析 (1)用待定系数法求出该抛物线的解析式即可;
(2)根据B、C、M的坐标,由勾股定理可求得△BCM三边的长,然后判断这三条边的长是否符合勾股定理的逆定理即可.
解答 解:(1)∵二次函数y=ax2+bx-3的图象与x轴交于A(-1,0),B(3,0)两点,
∴$\left\{\begin{array}{l}{a-b-3=0}\\{9a+3b-3=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=1}\\{b=-2}\end{array}\right.$,
则抛物线解析式为y=x2-2x-3;
(2)△BCM为直角三角形,理由如下:
对于抛物线解析式y=x2-2x-3=(x-1)2-4,即顶点M坐标为(1,-4),
令x=0,得到y=-3,即C(0,-3),
根据勾股定理得:BC=3$\sqrt{2}$,BM=2$\sqrt{5}$,CM=$\sqrt{2}$,
∴BM2=BC2+CM2,
∴△BCM为直角三角形.
点评 此题考查了二次函数解析式的求法、勾股定理、勾股定理的逆定理;熟练掌握勾股定理和逆定理是解决问题(2)的关键.

练习册系列答案
相关题目
6.某地一天早晨的气温是-5℃,中午上升了10℃,午夜又下降了8℃,则午夜的气温是( )
| A. | -3℃ | B. | -5℃ | C. | 5℃ | D. | -9℃ |
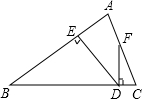 如图所示,△ABC中,AB=BC,DE⊥AB于点E,DF⊥BC于点D,交AC于F.
如图所示,△ABC中,AB=BC,DE⊥AB于点E,DF⊥BC于点D,交AC于F.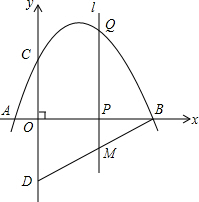 如图,抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2与x轴交于点A、点B,与y轴交于点C、点D与点C关于x轴对称,点P是x轴上一动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.
如图,抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2与x轴交于点A、点B,与y轴交于点C、点D与点C关于x轴对称,点P是x轴上一动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q. 如图,AB为⊙O的直径,弦AD平分∠CAB,过点D作DE⊥AC,垂足为点E,ED的延长线交AB的延长线于点F.
如图,AB为⊙O的直径,弦AD平分∠CAB,过点D作DE⊥AC,垂足为点E,ED的延长线交AB的延长线于点F.