题目内容
某市场对顾客实行优惠,规定:若一次购物不超过200元,则不给折扣;若一次购物超过200元,但不超过500元,按标价给予九折优惠;若一次购物超过500元,其中500元按上述九折优惠之外,超过500元的部分按八折优惠,某人两次购物分别付款168元和423元.
(1)第1次和第2次购买的商品分别标价多少元?
(2)若将第1次和第2次合起来去购买同样价值的商品,则他可节约多少元?
(3)张女士分两次从该市场购买了标价共为480元的商品,若她获得的优惠比合起来一次购买同样标价的商品获得的优惠少8元,又知她第一次购买的商品标价较高,你能求出张女士第一次购买商品花费了多少元吗?
答:张女士第一次购买商品付款 元(直接填空,不需写过程)
(1)第1次和第2次购买的商品分别标价多少元?
(2)若将第1次和第2次合起来去购买同样价值的商品,则他可节约多少元?
(3)张女士分两次从该市场购买了标价共为480元的商品,若她获得的优惠比合起来一次购买同样标价的商品获得的优惠少8元,又知她第一次购买的商品标价较高,你能求出张女士第一次购买商品花费了多少元吗?
答:张女士第一次购买商品付款
考点:一元一次方程的应用
专题:解题方法
分析:(1)某人两次去购物,分别付款168元与423元,由于商场的优惠规定,168元的商品未优惠,而423元的商品是按九折优惠后的,则实际商品价格为:423÷0.9=470元.应付款为:500×0.9+(638-500)×0.8=450+110.4=560.4(元).据此解答即可;
(2)他要一次购买的商品的价格为:168+470=638,应付款为:500×0.9+(638-500)×0.8=450+110.4=560.4(元).可节约168+423-560.4=30.6元;
(3)∵200<480<500,∴480元一次购买同样标价的商品获得的优惠为480×0.1=48元,则两次优惠48-8=40元,∴张女士分两次从该市场购买了标价共为480元的商品
,共花费440元,又知她第一次购买的商品标价较高,∴第一次享受九折优惠,第二次不享受优惠,设张女士第一次购买商品花费了x元,根据题意得:0.9x+(480-x)=440,解得:x=400.
(2)他要一次购买的商品的价格为:168+470=638,应付款为:500×0.9+(638-500)×0.8=450+110.4=560.4(元).可节约168+423-560.4=30.6元;
(3)∵200<480<500,∴480元一次购买同样标价的商品获得的优惠为480×0.1=48元,则两次优惠48-8=40元,∴张女士分两次从该市场购买了标价共为480元的商品
,共花费440元,又知她第一次购买的商品标价较高,∴第一次享受九折优惠,第二次不享受优惠,设张女士第一次购买商品花费了x元,根据题意得:0.9x+(480-x)=440,解得:x=400.
解答:解:(1)200×9=180,
∵168<180
∴第一次购物不享受优惠,第一次购买的标价为168元,
500×0.9=450元,
∵180<423<450,
∴第二次购物享受九折优惠,
∴设第二购物的标价为x元,
根据题意得:0.9x=423,
解得:x=470
∴第二次购买的标价为470元;
(2)他要一次购买的商品的价格为:168+470=638(元),
应付款为:
500×0.9+(638-500)×0.8
=450+110.4
=560.4(元).
168+423-560.4=30.6(元)
∴他可节约30.6元.
(3)480×0.9=432(元)‘
432+8=440(元)
∵她第一次购买的商品标价较高,
∴第一次享受九折优惠,第二次不享受优惠,
设张女士第一次购买商品花费了x元,
根据题意得:0.9x+(480-x)=440,
解得:x=400,
∴张女士第一次购买商品花费了400元.
∵168<180
∴第一次购物不享受优惠,第一次购买的标价为168元,
500×0.9=450元,
∵180<423<450,
∴第二次购物享受九折优惠,
∴设第二购物的标价为x元,
根据题意得:0.9x=423,
解得:x=470
∴第二次购买的标价为470元;
(2)他要一次购买的商品的价格为:168+470=638(元),
应付款为:
500×0.9+(638-500)×0.8
=450+110.4
=560.4(元).
168+423-560.4=30.6(元)
∴他可节约30.6元.
(3)480×0.9=432(元)‘
432+8=440(元)
∵她第一次购买的商品标价较高,
∴第一次享受九折优惠,第二次不享受优惠,
设张女士第一次购买商品花费了x元,
根据题意得:0.9x+(480-x)=440,
解得:x=400,
∴张女士第一次购买商品花费了400元.
点评:此题考查了分类讨论的思想的运用:分析实际付款可按不同方式打折.也考查了实际生活中的折扣问题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
轮船航行到A处时,观察到小岛B的方向是北偏西32°,那么同时从B处观测到轮船A的方向是( )
| A、南偏西32° |
| B、东偏南32° |
| C、南偏东58° |
| D、南偏东32° |
 如图,已知AC=AB,AE=AD,∠1=∠2.求证:∠DBC=∠ECB.
如图,已知AC=AB,AE=AD,∠1=∠2.求证:∠DBC=∠ECB. 已知,如图所示,在△ABC中,AB=AC,D是△ABC内一点,试证明:
已知,如图所示,在△ABC中,AB=AC,D是△ABC内一点,试证明: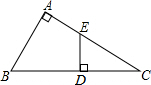 如图,在Rt△ABC中,∠A=90°,点D为斜边BC上一点,且BD=BA,过点D作BC的垂线交AC于点E.求证:AE=ED.
如图,在Rt△ABC中,∠A=90°,点D为斜边BC上一点,且BD=BA,过点D作BC的垂线交AC于点E.求证:AE=ED.