题目内容
11.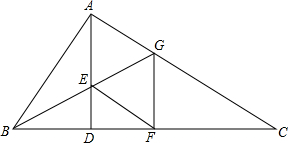 如图,AD是Rt△ABC斜边BC上的高,∠ABC的角平分线交AD于E,交AC于G.
如图,AD是Rt△ABC斜边BC上的高,∠ABC的角平分线交AD于E,交AC于G.(1)比较AE、AG的大小,并说明理由;
(2)作GF⊥BC于F,连结EF,判断四边形AEFG的形状,并说明理由;
(3)若AD=4,BD=3,求AE的长.
分析 (1)根据余角的性质得到∠AGE=∠BED,根据角平分线的定义得到∠ABG=∠DBG,等量代换得到∠BED=∠AGB,于是得到结论;
(2)根据角平分线的性质得到AG=GF,等量代换得到AE=FG,根据菱形的判定定理即可得到结论;
(3)根据余角的性质得到∠BAD=∠C,根据相似三角形的性质得到CD=$\frac{A{D}^{2}}{BD}$=$\frac{16}{3}$,根据勾股定理得到AC=$\sqrt{A{D}^{2}+C{D}^{2}}$=$\frac{20}{3}$,设AE=x,则AG=GF=x,根据相似三角形的性质即可得到结论.
解答 解:(1)AE=AG,
理由:∵AD是Rt△ABC斜边BC上的高,
∴∠ADB=∠BAC=90°,
∴∠ABG+∠AGB=∠DBG+∠BED=90°,
∴∠AGE=∠BED,
∵BG平分∠ABC,
∴∠ABG=∠DBG,
∴∠BED=∠AGB,
∵∠AEG=∠BED,
∴∠AEG=∠AGE,
∴AE=AG;
(2)四边形AEFG是菱形,
理由:∵GF⊥BC,GA⊥AB,BG平分∠ABC,
∴AG=GF,
∴AE=FG,
∵AD⊥BC,
∴AE∥FG,
∴四边形AEFG是菱形;
(3)∵∠BAC=90°,AD⊥BC,
∴∠BAD+∠DAC=∠DAC+∠C=90°,
∴∠BAD=∠C,
∴△ABD∽△ACD,
∴$\frac{AD}{BD}=\frac{CD}{AD}$,
∴CD=$\frac{A{D}^{2}}{BD}$=$\frac{16}{3}$,
∴AC=$\sqrt{A{D}^{2}+C{D}^{2}}$=$\frac{20}{3}$,
设AE=x,则AG=GF=x,
∵FG∥AD,
∴△CGF∽△CAD,
∴$\frac{FG}{AD}$=$\frac{CG}{AC}$,即$\frac{x}{4}$=$\frac{\frac{20}{3}-x}{\frac{20}{3}}$,
∴x=$\frac{5}{2}$,
∴AE=$\frac{5}{2}$.
点评 本题考查了菱形的判定和性质,相似三角形的判定和性质,等腰三角形的判定,勾股定理,角平分线的定义,正确是识别图形是解题的关键.

 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案现要选拨一人参赛:
| 甲 | 乙 | 丙 | |
| 代数 | 85 | 85 | 70 |
| 几何 | 92 | 80 | 83 |
| 综合 | 75 | 85 | 90 |
(2)若三次成绩按3:3:4的比例计算,应选谁参加?
(3)若三次成绩按20%,30%,50%计算,应选谁参加?
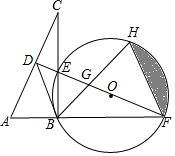 如图所示,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相交于点D,E,F.⊙O是△BEF的外接圆,∠EBF的平分线交EF于点G,交⊙O于点H,连接BD,FH.
如图所示,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相交于点D,E,F.⊙O是△BEF的外接圆,∠EBF的平分线交EF于点G,交⊙O于点H,连接BD,FH. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则抛物线与x轴的另一个交点坐标为(4,0).
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则抛物线与x轴的另一个交点坐标为(4,0). 如图,AD∥BE,AC,BC分别平分∠DAB和∠EBA,试判断AC和BC的位置关系,并说明理由.
如图,AD∥BE,AC,BC分别平分∠DAB和∠EBA,试判断AC和BC的位置关系,并说明理由.