题目内容
2．
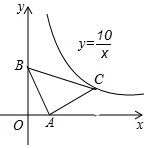如图，在△ABC中，AB=AC，∠BAC=90°，点A在x轴上，点B的坐标是（0，3），若点C恰好在反比例函数y=$\frac{10}{x}$第一象限内的图象上，那么点C的坐标为（5，2）．
分析 作CD⊥x轴于D，由于∠BAC=90°，容易求证△ABO≌△CAD，利用全等三角形的性质即可求出点C的坐标．
解答 
解：作CD⊥x轴于D，
∵∠BAC=90°
∴∠BAO+∠CAD=∠CAD+∠ACD=90°，
∴∠BAO=∠ACD
在△ABO与△CAD中
$\left\{\begin{array}{l}{∠AOB=∠ADC}\\{∠BAO=∠ACD}\\{AB=AC}\end{array}\right.$
∴△ABO≌△CAD（AAS）
∴OB=AD
设OA=a，
∵B（0，3）
∴OB=3，
∴AD=3，
∴OD=a+3，CD=OA=a，
∴C（a+3，a）
又∵点C在反比例函数y=$\frac{10}{x}$上
∴10=a（a+3）
解得：a=2或a=-5，
∴C（5，2）
故答案为：（5，2）
点评 本题考查反比例函数图象上点的特征，解题的关键是证明△ABO≌△CAD，利用AD=OB=3求出点C的坐标，本题属于中等题型．
练习册系列答案
相关题目
12．甲、乙、丙三位同学参加“华罗庚杯数学竞赛”培训．三个培训段的考试成绩如表：
现要选拨一人参赛：
（1）若按三次平均成绩选拔，应选谁参加？
（2）若三次成绩按3：3：4的比例计算，应选谁参加？
（3）若三次成绩按20%，30%，50%计算，应选谁参加？
现要选拨一人参赛：
| 甲 | 乙 | 丙 | |
| 代数 | 85 | 85 | 70 |
| 几何 | 92 | 80 | 83 |
| 综合 | 75 | 85 | 90 |
（2）若三次成绩按3：3：4的比例计算，应选谁参加？
（3）若三次成绩按20%，30%，50%计算，应选谁参加？
如图四边形ABCD中，AD∥BC，连接AC，E、F分别为AC、CB的中点，BC=2AD，S△CEF=2，四边形ABCD的面积为12．
如图，在Rt△ABC中，∠ABC=90°，AB是⊙O的直径，连接OC，过点A作AD∥OC交⊙O于点D，连接CD．
（1）如图1，菱形ABCD中，O是对角线AC上一点，连接OB，OD，求证：OB=OD．