题目内容
7.乐乐买了x块巧免力用了y元(其中x>10,y是整数),后来这种巧克力的价格每块降价10%,他比上次多买了2块巧克力,用了3元钱,则x的值是18.分析 设巧克力的原价为a元/块,则降价后的价格为0.9a元/块,根据总价=单价×数量,即可得出关于x、y、a的方程组,消去a后可得出x=$\frac{6y}{10-3y}$,由x>10、y为正数,即可求出y的取值范围,取其内的整数,将其代入x=$\frac{6y}{10-3y}$中,即可求出结论.
解答 解:设巧克力的原价为a元/块,则降价后的价格为0.9a元/块,
根据题意得:$\left\{\begin{array}{l}{ax=y①}\\{0.9a•(x+2)=3②}\end{array}\right.$,
①÷②得:$\frac{10x}{9(x+2)}$=$\frac{y}{3}$,
整理得:10x=3xy+6y,
∴x=$\frac{6y}{10-3y}$.
∵x>10,y为正数,
∴$\frac{6y}{10-3y}$>10且10-3y>0,
解得:$\frac{25}{9}$<y<$\frac{10}{3}$.
∵y为整数,
∴y=3,x=$\frac{6y}{10-3y}$=18.
故答案为:18.
点评 本题考查了分式方程的应用以及一元一次不等式的应用,根据总价=单价×数量,找出x=$\frac{6y}{10-3y}$是解题的关键.

练习册系列答案
相关题目
12.甲、乙、丙三位同学参加“华罗庚杯数学竞赛”培训.三个培训段的考试成绩如表:
现要选拨一人参赛:
(1)若按三次平均成绩选拔,应选谁参加?
(2)若三次成绩按3:3:4的比例计算,应选谁参加?
(3)若三次成绩按20%,30%,50%计算,应选谁参加?
现要选拨一人参赛:
| 甲 | 乙 | 丙 | |
| 代数 | 85 | 85 | 70 |
| 几何 | 92 | 80 | 83 |
| 综合 | 75 | 85 | 90 |
(2)若三次成绩按3:3:4的比例计算,应选谁参加?
(3)若三次成绩按20%,30%,50%计算,应选谁参加?
 如图,?ABCD中,E是AB的中点,连结CE并延长交DA的延长线于点F.求证:AF=AD.
如图,?ABCD中,E是AB的中点,连结CE并延长交DA的延长线于点F.求证:AF=AD.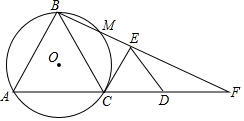 如图,C为线段AD上一点,△ABC和△CDE都是等边三角形,连接BE并延长,交AD长线于F,△ABC的外接圆⊙O交BF于点M.
如图,C为线段AD上一点,△ABC和△CDE都是等边三角形,连接BE并延长,交AD长线于F,△ABC的外接圆⊙O交BF于点M. 如图是某晚报“百姓热线”一周内接到热线电话的统计图,其中有关环境保护的问题的电话最多,共70个,请回答下列问题.
如图是某晚报“百姓热线”一周内接到热线电话的统计图,其中有关环境保护的问题的电话最多,共70个,请回答下列问题.


