题目内容
6. 一次函数y=kx+k的图象与函数y=|x-1|的图象有两个交点,则k的取值范围是0<k<1.
一次函数y=kx+k的图象与函数y=|x-1|的图象有两个交点,则k的取值范围是0<k<1.
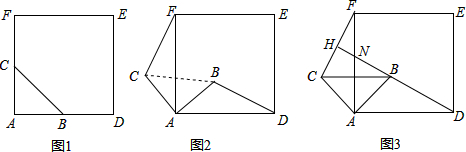
分析 由题意可知:y=kx+k=k(x+1)恒过(-1,0),由于直线y=kx+k的图象与函数y=|x-1|的图象有两个交点,结合图象即可求出k的范围.
解答  解:由题意可知:y=kx+k=k(x+1)恒过(-1,0),
解:由题意可知:y=kx+k=k(x+1)恒过(-1,0),
如图所示,当k<0时,此时直线y=kx+k的图象与函数y=|x-1|的图象交点不多于1个,
∴k>0,
由于直线y=kx+k的图象与函数y=|x-1|的图象有两个交点,
∴直线y=kx+k不能与y=x-1平行,
∴k<1,
∴0<k<1,
故答案为:0<k<1
点评 本题考查一次函数的综合问题,解题的关键是y=kx+k=k(x+1)恒过(-1,0),然后利用数形结合的思想求出k的范围,本题属于中等题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.已知点A(-1,0),B(2,0),在y轴上存在一点C,使三角形ABC的面积为6,则点C的坐标为( )
| A. | (0,4) | B. | (0,2) | C. | (0,2)或(0,-2) | D. | (0,4)或(0,-4) |
15.近年来空气净化器成为很多家庭的新电器.某品牌的空气净化器厂家为进一步了解市场,制定生产计划,根据2016年下半年销售情况绘制了统计表,其中同比增长率=($\frac{当月销售量}{去年同月销售量}$-1)×100%,下面有四个推断:
①2016年下半年各月销售量均比2015年同月销售量增多;
②2016年下半年销售量增长幅度最大的是11月至12月;
③2015年9月的销售量约为9.3万台;
④若保持相同的增长率,则2017年10月的销售量可约为15.4万台;
其中正确的是( )
①2016年下半年各月销售量均比2015年同月销售量增多;
②2016年下半年销售量增长幅度最大的是11月至12月;
③2015年9月的销售量约为9.3万台;
④若保持相同的增长率,则2017年10月的销售量可约为15.4万台;
其中正确的是( )
| 7月 | 8月 | 9月 | 10月 | 11月 | 12月 | |
| 销售量 | 8 | 9.3 | 9.8 | 13.4 | 19.7 | 36 |
| 同比增长率 | -2.3% | 6.5% | 5.2% | 15.1% | 20.7% | 35.9% |
| A. | ①③④ | B. | ②③④ | C. | ②③ | D. | ②④ |
 如图,正六边形ABCDEF内接于⊙O,⊙O的半径为6,则这个正六边形的边心距OM的长为3$\sqrt{3}$.
如图,正六边形ABCDEF内接于⊙O,⊙O的半径为6,则这个正六边形的边心距OM的长为3$\sqrt{3}$.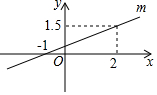 如图所示,直线m是一次函数y=kx+b的图象.
如图所示,直线m是一次函数y=kx+b的图象. 如图,在平面直角坐标系中,直线l1:y=-$\frac{1}{2}$x+6与x轴、y轴交于点B、C,且与直线l2:y=$\frac{1}{2}$x交于点A.
如图,在平面直角坐标系中,直线l1:y=-$\frac{1}{2}$x+6与x轴、y轴交于点B、C,且与直线l2:y=$\frac{1}{2}$x交于点A.