题目内容
19.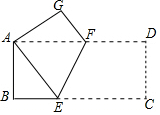 如图,矩形纸片ABCD中,AB=4,BC=8,将纸片沿EF折叠,使点C与点A重合,则△AEF的面积是( )
如图,矩形纸片ABCD中,AB=4,BC=8,将纸片沿EF折叠,使点C与点A重合,则△AEF的面积是( )| A. | 8 | B. | 10 | C. | 12 | D. | 14 |
分析 由折叠的性质可得,AD'=CD=AB=4,设AE=x,则DE=D'E=8-x,根据勾股定理即可求解.
解答 解:由折叠的性质可得,AD'=CD,DE=D'E,
∵CD=AB,AB=4,
∴AD'=CD=4
设AE=x,则DE=D'E=8-x,
在Rt△AD'E中,x2-(8-x)2=42,
解得,x=5,
即AE=5,
∴△AEF的面积=$\frac{1}{2}$AE•AB=$\frac{1}{2}×$5×4=10,
故选B.
点评 本题考查了翻折变换、勾股定理及矩形的性质,熟练掌握折叠的性质是解题的关键.

练习册系列答案
相关题目
14.下列实数中:$\sqrt{36}$、$\sqrt{11}$、1.414、$\frac{22}{5}$、0.1010010001…(往后每两个1之间依次多一个0)、π,无理数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
4.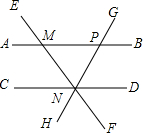 如图,AB∥CD,直线EF与AB,CD分别交于点 M,N,过点N的直线GH 与AB交于点P,则下列结论中一定正确的个数是( )
如图,AB∥CD,直线EF与AB,CD分别交于点 M,N,过点N的直线GH 与AB交于点P,则下列结论中一定正确的个数是( )
①∠EMB=∠MND;②∠BMN=∠MNC;③∠CNH=∠BPG;④∠DNG=∠AME.
 如图,AB∥CD,直线EF与AB,CD分别交于点 M,N,过点N的直线GH 与AB交于点P,则下列结论中一定正确的个数是( )
如图,AB∥CD,直线EF与AB,CD分别交于点 M,N,过点N的直线GH 与AB交于点P,则下列结论中一定正确的个数是( )①∠EMB=∠MND;②∠BMN=∠MNC;③∠CNH=∠BPG;④∠DNG=∠AME.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
8. 如图,直线AB、CD相交于点O,OE⊥AB于O,∠EOC=35°,则∠AOD的度数为( )
如图,直线AB、CD相交于点O,OE⊥AB于O,∠EOC=35°,则∠AOD的度数为( )
 如图,直线AB、CD相交于点O,OE⊥AB于O,∠EOC=35°,则∠AOD的度数为( )
如图,直线AB、CD相交于点O,OE⊥AB于O,∠EOC=35°,则∠AOD的度数为( )| A. | 35° | B. | 55° | C. | 115° | D. | 125° |
 如图,在平面直角坐标系中:A(1,1),B(-1,1),C(-1,-2),D(1,-2),现把一条长为2018个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A→B→C→D→A→…的规律紧绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是(1,-1).
如图,在平面直角坐标系中:A(1,1),B(-1,1),C(-1,-2),D(1,-2),现把一条长为2018个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A→B→C→D→A→…的规律紧绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是(1,-1).