题目内容
11.(1)解方程组:$\left\{\begin{array}{l}{2x-3y=1}\\{x+2y=4}\end{array}\right.$(2)解不等式$\frac{x}{6}$-1>$\frac{x-2}{3}$,并把它的解集在数轴上表示出来.
分析 (1)加减消元法求解可得;
(2)根据解一元一次不等式基本步骤:去分母、去括号、移项、合并同类项、系数化为1可得.
解答 解:(1)$\left\{\begin{array}{l}{2x-3y=1}&{①}\\{x+2y=4}&{②}\end{array}\right.$,
①-②×2,得:-7y=-7,
解得:y=1,
将y=1代入②,得:x+2=4,即x=2,
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$;
(2)去分母,得:x-6>2(x-2),
去括号,得:x-6>2x-4,
移项,得:x-2x>-4+6,
合并同类项,得:-x>2,
系数化为1,得:x<-2,
将解集表示在数轴上如下:
点评 本题主要考查解二元一次方程组和解一元一次不等式的基本能力,严格遵循解不等式的基本步骤是关键,尤其需要注意不等式两边都乘以或除以同一个负数不等号方向要改变.

练习册系列答案
相关题目
1.下列根式中,属于最简二次根式的是( )
| A. | $\sqrt{2}$ | B. | $\sqrt{4}$ | C. | $\sqrt{8}$ | D. | $\sqrt{9}$ |
2.若关于x的方程x-2+3k=$\frac{x+k}{3}$的解是正数,则k的取值范围是( )
| A. | k>$\frac{3}{4}$ | B. | k≥$\frac{3}{4}$ | C. | k<$\frac{3}{4}$ | D. | k≤$\frac{3}{4}$ |
19.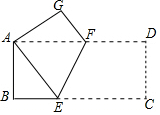 如图,矩形纸片ABCD中,AB=4,BC=8,将纸片沿EF折叠,使点C与点A重合,则△AEF的面积是( )
如图,矩形纸片ABCD中,AB=4,BC=8,将纸片沿EF折叠,使点C与点A重合,则△AEF的面积是( )
 如图,矩形纸片ABCD中,AB=4,BC=8,将纸片沿EF折叠,使点C与点A重合,则△AEF的面积是( )
如图,矩形纸片ABCD中,AB=4,BC=8,将纸片沿EF折叠,使点C与点A重合,则△AEF的面积是( )| A. | 8 | B. | 10 | C. | 12 | D. | 14 |
16.下列代数式中是分式的为( )
| A. | $\frac{x}{x+2}$ | B. | $\frac{{x}^{2}-2}{π}$ | C. | $\frac{4x}{7}$ | D. | $\frac{3-x}{4}$ |
3.根据下列表述,能确定具体位置的是( )
| A. | 某电影院2排 | B. | 大桥南路 | ||
| C. | 北偏东30° | D. | 东经108°,北纬43° |
20.有下列实数:$\frac{22}{7}$,-3.14159,$\sqrt{8}$,0,$\root{3}{27}$,0.$\stackrel{•}{3}\stackrel{•}{1}$,$\frac{π}{2}$,其中无理数的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
1.以下说法合理的是( )
| A. | 小明在10次抛图钉的试验中发现3次钉尖朝上,由此他说钉尖朝上的概率是30% | |
| B. | 掷一枚骰子,掷出点6的概率是$\frac{1}{6}$,意思是每掷6次就有1次掷得点数为6 | |
| C. | 某彩票的中奖机会是2%,那么买100张彩票一定会有2张中奖 | |
| D. | 甲、乙两组同学分别进行抛掷硬币的试验,正面朝上的频率分别为0.48和0.51 |