题目内容
函数y=-
x+1的图象与x轴交于A,与y轴交于B,C在直线AB上,且OC=
AB,反比例函数y=
过C点,则k的值可能是 .
| 1 |
| 2 |
| 1 |
| 2 |
| k |
| x |
考点:反比例函数与一次函数的交点问题
专题:
分析:首先求出点A、B的坐标,然后由“直角三角形斜边上的中线等于斜边的一半”确定点C是线段AB的中点,据此可以求得点C的坐标,把点C的坐标代入反比例函数解析式即可求得k的值.另外,以点O为圆心,OC长为半径作圆,与直线AB有另外一个交点C′,点C′也符合要求,不要遗漏.
解答: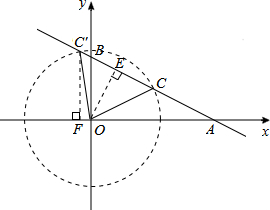 解:在y=-
解:在y=-
x+1中,令y=0,则x=2;令x=0,得y=1,
∴A(2,0),B(0,1).
在Rt△AOB中,由勾股定理得:AB=
=
,则OC=
AB=
.
方法一:设∠BAO=θ,则sinθ=
=
=
,cosθ=
=
=
.
当点C为线段AB中点时,有OC=
AB=
.
∵A(2,0),B(0,1),
∴C(1,
).
以点O为圆心,OC长为半径作圆,与直线AB的另外一个交点是C′,则点C、点C′均符合条件.
如图,过点O作OE⊥AB于点E,则AE=OA•cosθ=2×
=
,
∴EC=AE-AC=
-
=
.
∵OC=OC′,∴EC′=EC=
,
∴AC′=AE+EC′=
+
=
.
过点C′作CF⊥x轴于点F,则C′F=AC′•sinθ=
×
=
,
AF=AC′•cosθ=
×
=
,
∴OF=AF-OA=
-2=
.
∴C′(-
,
).
∵反比例函数y=
的图象经过点C或C′,1×
=
,-
×
=-
,
∴k=
或-
.
方法二:设C(m,-
m+1),
∵OC=
,
∴m2+(-
m+1)2=(
)2,
解得:m=-
或1.
∴C(-
,
)或(1,
).
∴k=
或-
.
故答案为:
或-
.
 解:在y=-
解:在y=-| 1 |
| 2 |
∴A(2,0),B(0,1).
在Rt△AOB中,由勾股定理得:AB=
| OA2+OB2 |
| 5 |
| 1 |
| 2 |
| ||
| 2 |
方法一:设∠BAO=θ,则sinθ=
| OB |
| AB |
| 1 | ||
|
| ||
| 5 |
| OA |
| AB |
| 2 | ||
|
2
| ||
| 5 |
当点C为线段AB中点时,有OC=
| 1 |
| 2 |
| ||
| 2 |
∵A(2,0),B(0,1),
∴C(1,
| 1 |
| 2 |
以点O为圆心,OC长为半径作圆,与直线AB的另外一个交点是C′,则点C、点C′均符合条件.
如图,过点O作OE⊥AB于点E,则AE=OA•cosθ=2×
2
| ||
| 5 |
4
| ||
| 5 |
∴EC=AE-AC=
4
| ||
| 5 |
| ||
| 2 |
3
| ||
| 10 |
∵OC=OC′,∴EC′=EC=
3
| ||
| 10 |
∴AC′=AE+EC′=
4
| ||
| 5 |
3
| ||
| 10 |
11
| ||
| 10 |
过点C′作CF⊥x轴于点F,则C′F=AC′•sinθ=
11
| ||
| 10 |
| ||
| 5 |
| 11 |
| 10 |
AF=AC′•cosθ=
11
| ||
| 10 |
2
| ||
| 5 |
| 11 |
| 5 |
∴OF=AF-OA=
| 11 |
| 5 |
| 1 |
| 5 |
∴C′(-
| 1 |
| 5 |
| 11 |
| 10 |
∵反比例函数y=
| k |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 5 |
| 11 |
| 10 |
| 11 |
| 50 |
∴k=
| 1 |
| 2 |
| 11 |
| 50 |
方法二:设C(m,-
| 1 |
| 2 |
∵OC=
| ||
| 2 |
∴m2+(-
| 1 |
| 2 |
| ||
| 2 |
解得:m=-
| 1 |
| 5 |
∴C(-
| 1 |
| 5 |
| 11 |
| 10 |
| 1 |
| 2 |
∴k=
| 1 |
| 2 |
| 11 |
| 50 |
故答案为:
| 1 |
| 2 |
| 11 |
| 50 |
点评:本题考查了反比例函数与一次函数的交点问题.注意符合条件的C点有两个,需要分别计算,不要遗漏.

练习册系列答案
相关题目
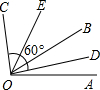 如图,∠AOB:∠BOC=3:5,又OD、OE分别是∠AOB和∠BOC的平分线,若∠DOC=60°,求∠AOB和∠BOC的度数.
如图,∠AOB:∠BOC=3:5,又OD、OE分别是∠AOB和∠BOC的平分线,若∠DOC=60°,求∠AOB和∠BOC的度数. 如图,AB•AE=AC•AD,∠1=∠2,求证:∠B=∠D.
如图,AB•AE=AC•AD,∠1=∠2,求证:∠B=∠D. 如图,∠DOE:∠BOE=1:2,∠DOC:∠COA=1:2,如果∠AOB=120°,那么∠EOC是多少度?
如图,∠DOE:∠BOE=1:2,∠DOC:∠COA=1:2,如果∠AOB=120°,那么∠EOC是多少度?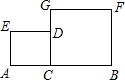 如图,已知线段AB=6,在线段AB上有一点C(不同于A、B),分别以AC、BC为边在AB同侧作正方形ACDE、CBFG,设AC=x.
如图,已知线段AB=6,在线段AB上有一点C(不同于A、B),分别以AC、BC为边在AB同侧作正方形ACDE、CBFG,设AC=x.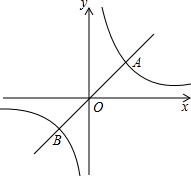 如图,定义:若双曲线y=
如图,定义:若双曲线y=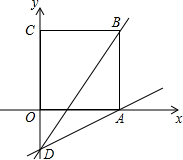 已知在平面直角坐标系中,点O为坐标原点,直线y=
已知在平面直角坐标系中,点O为坐标原点,直线y=