题目内容
17.甲、乙两个学习小组各有4名同学,在某次测验中,他们的得分情况如下表所示:| 组员1 | 组员2 | 组员3 | 组员4 | |
| 甲 | 88 | 95 | 97 | 100 |
| 乙 | 90 | 94 | 97 | 99 |
| A. | X甲=X乙,S2甲>S2乙 | B. | X甲=X乙,S2甲<S2乙 | ||
| C. | X甲<X乙,S2甲>S2乙 | D. | X甲<X乙,S2甲<S2乙 |
分析 根据算术平均数的计算公式和方差的计算公式:平均数为$\overline{x}$,则方差S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2],分别求出X甲、X乙和S2甲、S2乙,比较即可得到答案.
解答 解:X甲=$\frac{1}{4}$(88+95+97+100)=95,
S2甲=$\frac{1}{4}$[(88-95)2+(95-95)2+(97-95)2+(100-95)2]=19.5,
X乙=$\frac{1}{4}$(90+94+97+99)=95,
S2乙=$\frac{1}{4}$[(90-95)2+(94-95)2+(97-95)2+[(99-95)2]=11.5,
故选:A.
点评 本题考查的是算术平均数和方差的计算,掌握各自的计算公式是解题的关键,如果一组数据平均数为$\overline{x}$,则方差S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2].

练习册系列答案
相关题目
10.下列选项中,∠MOP与∠NOP是邻补角的是( )
| A. |  | B. |  | C. |  | D. |  |
9.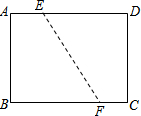 如图,矩形ABCD的边长AB=6,BC=8,将矩形沿EF折叠,使B点与D点重合,则折痕EF的长是( )
如图,矩形ABCD的边长AB=6,BC=8,将矩形沿EF折叠,使B点与D点重合,则折痕EF的长是( )
 如图,矩形ABCD的边长AB=6,BC=8,将矩形沿EF折叠,使B点与D点重合,则折痕EF的长是( )
如图,矩形ABCD的边长AB=6,BC=8,将矩形沿EF折叠,使B点与D点重合,则折痕EF的长是( )| A. | 6 | B. | $\frac{15}{4}$ | C. | 5 | D. | $\frac{15}{2}$ |
5.设a1,a2,…,a10是从1,0,-1这三个数中取值的一列数,若a1+a2+…+a10=1,(a1+1)2+(a2+1)2+…+(a10+1)2=17,则a1,a2,…,a10中1的个数为( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
6.已知a,b,c均为实数,且a>b,c≠0,则下列结论不一定正确的是( )
| A. | a+c>b+c | B. | -a<-b | C. | a2>b2 | D. | $\frac{a}{{c}^{2}}$>$\frac{b}{{c}^{2}}$ |