题目内容
16．已知点A、点B．在网格中用无刻度直尺画两个不全等的菱形，使菱形的顶点A、B、C、D恰好为格点，并计算所画菱形面积．
分析 由勾股定理得出AB=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$，根据菱形的性质以及格点的位置作图即可．
解答 解：如图，
第一个菱形的面积为8，第二个菱形的面积为6．
点评 此题主要考查了作图-应用与设计作图，首先要理解题意，弄清问题中对所作图形的要求，结合对应几何图形的性质和基本作图的方法作图．
练习册系列答案
相关题目
6．两条抛物线y1=-$\frac{1}{2}$x2+b，y2=-$\frac{1}{2}$x2-b与分别经过点（-2，0），（2，0）且平行于y轴的两条平行线围成的部分的面积为8，则b等于（ ）
| A． | 1 | B． | -3 | C． | 4 | D． | -1或3 |
4．
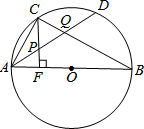已知，如图Rt△ABC内接于⊙O，AB为直径，CF⊥AB，tan∠ABC=$\frac{3}{4}$，CF=8，D是$\widehat{BC}$的中点，BC与AD的交点为Q，则$\frac{AQ}{DQ}$等于（ ）
已知，如图Rt△ABC内接于⊙O，AB为直径，CF⊥AB，tan∠ABC=$\frac{3}{4}$，CF=8，D是$\widehat{BC}$的中点，BC与AD的交点为Q，则$\frac{AQ}{DQ}$等于（ ）| A． | 2.8 | B． | 3 | C． | 3.5 | D． | 4 |
11．下列运算中正确的是（ ）
| A． | （a-b）2=a2-b2 | B． | （-a+1）（-a-1）=a2-1 | C． | （-$\frac{1}{2}$）-2=1 | D． | -（-2ab2）2=4a2b4 |
1．下列运算正确的是（ ）
| A． | （a2）3=a5 | B． | a2+a4=a6 | C． | a3÷a3=1 | D． | （a3-a）÷a=a2 |
6．化简$\sqrt{36×144}$，正确的结果是（ ）
| A． | ±72 | B． | 72 | C． | 432 | D． | 以上答案都不是 |