题目内容
8．用一根长为32cm的铁丝围成一个矩形，则围成矩形面积的最大值是64cm2．分析 设矩形的一边长是xcm，则邻边的长是（16-x）cm，则矩形的面积S即可表示成x的函数，根据函数的性质即可求解．
解答 解：设矩形的一边长是xcm，则邻边的长是（16-x）cm．
则矩形的面积S=x（16-x），即S=-x2+16x，
当x=-$\frac{b}{2a}$=-$\frac{16}{-2}$=8时，S有最大值是：64．
故答案是：64．
点评 本题考查了二次函数的性质，求最值得问题常用的思路是转化为函数问题，利用函数的性质求解．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
18．
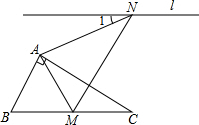如图，含有30°的直角三角板△ABC，∠BAC=90°，∠C=30°，将△ABC绕着点A逆时针旋转，得到△AMN，使得点B落在BC边上的点M处，过点N的直线l∥BC，则∠1的度数为（ ）
如图，含有30°的直角三角板△ABC，∠BAC=90°，∠C=30°，将△ABC绕着点A逆时针旋转，得到△AMN，使得点B落在BC边上的点M处，过点N的直线l∥BC，则∠1的度数为（ ）| A． | 15° | B． | 30° | C． | 45° | D． | 60° |
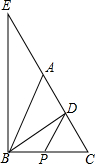如图，在△ABC中，AB=AC，BD⊥AC于点D，过点B作BE⊥BC交CA的延长线于点E，点P是BC的中点，连接PD，则下列结论：①∠BAC=2∠DBC；②BC2=2CD•AB；③若BC=15，BD=12，则AD=$\frac{7}{2}$；④图中一定相似的三角形有5对，其中正确结论的个数是（ ）
3．命题“关于x的一元二次方程x2+bx+1=0，必有实数解．”是假命题．则在下列选项中，可以作为反例的是（ ）
| A． | b=-3 | B． | b=-2 | C． | b=-1 | D． | b=2 |
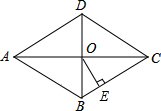如图，在菱形ABCD中，对角线AC与BD相交于点O，AC=8，BD=6，OE⊥BC，垂足为点E，则OE=$\frac{12}{5}$．