题目内容
2. 如图,把一个直角三角尺ACB绕着30°角的顶点B顺时针旋转,使得点A与CB的延长线上的点E重合.
如图,把一个直角三角尺ACB绕着30°角的顶点B顺时针旋转,使得点A与CB的延长线上的点E重合.(1)三角尺旋转了150度;
(2)点C对应的点是D,线段AB的对应线段是EB;
(3)若AC=$\sqrt{3}$cm,求在旋转过程中,点C走过的路径长.
分析 (1)由点A与CB的延长线上的点E重合可得到∠ABE的度数,从而得出旋转角的角度;
(2)从图象特征可以得出对应点及对应线段;
(3)点C走过的路径即为以点B为圆心,BC长为半径的一段弧长,求出BC的长再结合旋转角,就可以求出.
解答 解:(1)∵三角形旋转后点A与CB的延长线上的点E重合,∠ABC=30°,
∴∠ABC=150°.
故答案为:150;
(2)∵由题可知点A对应点为E,绕点B旋转;
∴点C对应点为D.
故答案为:D,BE;
(3)由题可知,点C走过的路程是以点B为圆心,BC长为半径的一段弧长
∵AC=$\sqrt{3}$,∠CBD=150°,
∴点C走过的路径长=$\frac{\sqrt{3}•π•150°}{180°}$=$\frac{5\sqrt{3}π}{6}$cm.
点评 本题考查了旋转的性质、直角三角形性质、勾股定理及弧长计算公式,解题的关键是确定旋转角的度数及对应点.

练习册系列答案
相关题目
9.sin60°的值等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
6.已知正六边形的边长为2,则它的内切圆的半径为( )
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{3}$ |
13.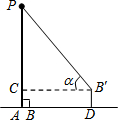 小明利用测角仪和旗杆的拉绳测量学校旗杆的高度.如图,旗杆PA的高度与拉绳PB的长度相等.小明将PB拉到PB′的位置,测得∠PB′C=α(B′C为水平线),测角仪B′D的高度为1米,则旗杆PA的高度为( )
小明利用测角仪和旗杆的拉绳测量学校旗杆的高度.如图,旗杆PA的高度与拉绳PB的长度相等.小明将PB拉到PB′的位置,测得∠PB′C=α(B′C为水平线),测角仪B′D的高度为1米,则旗杆PA的高度为( )
 小明利用测角仪和旗杆的拉绳测量学校旗杆的高度.如图,旗杆PA的高度与拉绳PB的长度相等.小明将PB拉到PB′的位置,测得∠PB′C=α(B′C为水平线),测角仪B′D的高度为1米,则旗杆PA的高度为( )
小明利用测角仪和旗杆的拉绳测量学校旗杆的高度.如图,旗杆PA的高度与拉绳PB的长度相等.小明将PB拉到PB′的位置,测得∠PB′C=α(B′C为水平线),测角仪B′D的高度为1米,则旗杆PA的高度为( )| A. | $\frac{1}{1-sinα}$ | B. | $\frac{1}{1+sinα}$ | C. | $\frac{1}{1-cosα}$ | D. | $\frac{1}{1+cosα}$ |
7.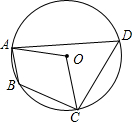 如图,四边形ABCD内接于⊙O,若∠AOC=100°,则∠ABC的大小为( )
如图,四边形ABCD内接于⊙O,若∠AOC=100°,则∠ABC的大小为( )
 如图,四边形ABCD内接于⊙O,若∠AOC=100°,则∠ABC的大小为( )
如图,四边形ABCD内接于⊙O,若∠AOC=100°,则∠ABC的大小为( )| A. | 100° | B. | 50° | C. | 130° | D. | 80° |
14.下列各组中的两个图形,不一定相似的是( )
| A. | 有一个角是120°的两个等腰三角形 | B. | 两个等边三角形 | ||
| C. | 两个直角三角形 | D. | 两个等腰直角三角形 |
12.一次数学测试后,某班40名学生的成绩被分为5组,第1~4组的频数分别为12、10、6、8,则第5组的频率是( )
| A. | 0.1 | B. | 0.2 | C. | 0.3 | D. | 0.4 |
 如图,AB是⊙O的直径,点P是弦AC上一动点(不与A,C重合),过点P作PE⊥AB,垂足为E,射线EP交$\widehat{AC}$于点F,交过点C的切线于点D.
如图,AB是⊙O的直径,点P是弦AC上一动点(不与A,C重合),过点P作PE⊥AB,垂足为E,射线EP交$\widehat{AC}$于点F,交过点C的切线于点D. 某农场拟建三间长方形种牛饲养室,饲养室的一面靠墙(墙长50m),中间用两道墙隔开(如图).已知计划中的建筑材料可建墙的总长度为48m,则这三间长方形种牛饲养室的总占地面积的最大值为144m2.
某农场拟建三间长方形种牛饲养室,饲养室的一面靠墙(墙长50m),中间用两道墙隔开(如图).已知计划中的建筑材料可建墙的总长度为48m,则这三间长方形种牛饲养室的总占地面积的最大值为144m2.