题目内容
8. 如图,AB是⊙O的直径,点P是弦AC上一动点(不与A,C重合),过点P作PE⊥AB,垂足为E,射线EP交$\widehat{AC}$于点F,交过点C的切线于点D.
如图,AB是⊙O的直径,点P是弦AC上一动点(不与A,C重合),过点P作PE⊥AB,垂足为E,射线EP交$\widehat{AC}$于点F,交过点C的切线于点D.(1)求证:DC=DP;
(2)若∠CAB=30°,当F是$\widehat{AC}$的中点时,判断以A,O,C,F为顶点的四边形是什么特殊四边形?说明理由.
分析 (1)连接OC,根据切线的性质和PE⊥OE以及∠OAC=∠OCA得∠APE=∠DPC,然后结合对顶角的性质可证得结论;
(2)由∠CAB=30°易得△OBC为等边三角形,可得∠AOC=120°,由F是$\widehat{AC}$的中点,易得△AOF与△COF均为等边三角形,可得AF=AO=OC=CF,易得以A,O,C,F为顶点的四边形是菱形.
解答 (1)证明:连接OC,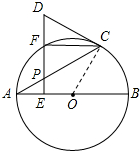
∵∠OAC=∠ACO,PE⊥OE,OC⊥CD,
∴∠APE=∠PCD,
∵∠APE=∠DPC,
∴∠DPC=∠PCD,
∴DC=DP;
(2)解:以A,O,C,F为顶点的四边形是菱形;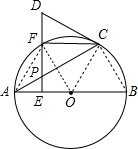
∵∠CAB=30°,∴∠B=60°,
∴△OBC为等边三角形,
∴∠AOC=120°,
连接OF,AF,
∵F是$\widehat{AC}$的中点,
∴∠AOF=∠COF=60°,
∴△AOF与△COF均为等边三角形,
∴AF=AO=OC=CF,
∴四边形OACF为菱形.
点评 本题主要考查了切线的性质、圆周角定理和等边三角形的判定等,作出恰当的辅助线利用切线的性质是解答此题的关键.

练习册系列答案
相关题目
18.下列运算正确的是( )
| A. | (-2a3)2=-4a6 | B. | $\sqrt{9}$=±3 | C. | m2•m3=m6 | D. | x3+2x3=3x3 |
19.月球的直径约为3476000米,将3476000用科学记数法表示应为( )
| A. | 0.3476×102 | B. | 34.76×104 | C. | 3.476×106 | D. | 3.476×108 |
20.“数学是将科学现象升华到科学本质认识的重要工具”,比如在化学中,甲烷的化学式CH4,乙烷的化学式是C2H6,丙烷的化学式是C3H8,…,设碳原子的数目为n(n为正整数),则它们的化学式都可用下列哪个式子来表示( )
| A. | CnH2n+2 | B. | CnH2n | C. | CnH2n-2 | D. | CnHn+3 |
17.关于x的一元二次方程x2+4x+k=0有两个相等的实根,则k的值为( )
| A. | k=-4 | B. | k=4 | C. | k≥-4 | D. | k≥4 |
 如图,在平面直角坐标系中,△ABC的顶点A(0,1),B(3,2),C(1,4)均在正方形网格的格点上.
如图,在平面直角坐标系中,△ABC的顶点A(0,1),B(3,2),C(1,4)均在正方形网格的格点上. 如图所示,△ABC中,∠BAC=33°,将△ABC绕点A按顺时针方向旋转50°,对应得到△AB′C′,则∠B′AC的度数为17°.
如图所示,△ABC中,∠BAC=33°,将△ABC绕点A按顺时针方向旋转50°,对应得到△AB′C′,则∠B′AC的度数为17°. 如图,把一个直角三角尺ACB绕着30°角的顶点B顺时针旋转,使得点A与CB的延长线上的点E重合.
如图,把一个直角三角尺ACB绕着30°角的顶点B顺时针旋转,使得点A与CB的延长线上的点E重合.