题目内容
6.已知正六边形的边长为2,则它的内切圆的半径为( )| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{3}$ |
分析 根据题意画出图形,利用正六边形中的等边三角形的性质求解即可.
解答 解:如图,连接OA、OB,OG;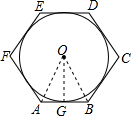
∵六边形ABCDEF是边长为2的正六边形,
∴△OAB是等边三角形,
∴OA=AB=2,
∴OG=OA•sin60°=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
∴边长为2的正六边形的内切圆的半径为$\sqrt{3}$.
故选B.
点评 本题考查学生对正多边形的概念掌握和计算的能力.解答这类题往往一些学生因对正多边形的基本知识不明确,将多边形的半径与内切圆的半径相混淆而造成错误计算,记住基本概念是解题的关键,属于中考常考题型.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
17.关于x的一元二次方程x2+4x+k=0有两个相等的实根,则k的值为( )
| A. | k=-4 | B. | k=4 | C. | k≥-4 | D. | k≥4 |
1.一个不透明的袋中,装有2个黄球、3个红球和5个白球,它们除颜色外都相同.从袋中任意摸出一个球,是白球的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{10}$ | D. | $\frac{1}{5}$ |
11.下列运算正确的是( )
| A. | 2x+y=2xy | B. | x•2y2=2xy2 | C. | 2x÷x2=2x | D. | 4x-5x=-1 |
 如图,在平面直角坐标系中,△ABC的顶点A(0,1),B(3,2),C(1,4)均在正方形网格的格点上.
如图,在平面直角坐标系中,△ABC的顶点A(0,1),B(3,2),C(1,4)均在正方形网格的格点上. 如图,把一个直角三角尺ACB绕着30°角的顶点B顺时针旋转,使得点A与CB的延长线上的点E重合.
如图,把一个直角三角尺ACB绕着30°角的顶点B顺时针旋转,使得点A与CB的延长线上的点E重合.
 如图,AC是正五边形ABCDE的一条对角线,则∠ACB=36°.
如图,AC是正五边形ABCDE的一条对角线,则∠ACB=36°.