题目内容

7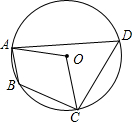．如图，四边形ABCD内接于⊙O，若∠AOC=100°，则∠ABC的大小为（　　）
A．100°B．50°C．130°D．80°

分析 先依据圆周角定理求得∠D的度数，然后再依据圆内接四边形的性质求得∠ABC的度数即可．

解答 解：∵∠D=$\frac{1}{2}$∠AOC，∠AOC=100°，
∴∠D=50°．
∵四边形ABCD内接于⊙O，
∴∠B+∠D=180°．
∴∠B=180°-50°=130°．
故选：C．

点评 本题主要考查的是圆内接四边形的性质、圆周角定理的应用，求得∠D的度数是解题的关键．

练习册系列答案
相关题目
13．不等式组$\left\{\begin{array}{l}{x+2＞1}\\{2x-1≤8-x}\end{array}\right.$的最大整数解是3．
14．计算（$\sqrt{5}$+$\sqrt{3}$）（$\sqrt{5}$-$\sqrt{3}$）的结果等于2．
11．下列运算正确的是（　　）
A．2x+y=2xyB．x•2y2=2xy2C．2x÷x2=2xD．4x-5x=-1
2．如图，把一个直角三角尺ACB绕着30°角的顶点B顺时针旋转，使得点A与CB的延长线上的点E重合．
（1）三角尺旋转了150度；
（2）点C对应的点是D，线段AB的对应线段是EB；
（3）若AC=$\sqrt{3}$cm，求在旋转过程中，点C走过的路径长．
12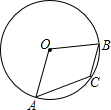．如图，⊙O中，劣弧AB所对的圆心角∠AOB=120°，点C在劣弧AB上，则圆周角∠ACB=（　　）
A．60°B．120°C．135°D．150°
19．如图1，抛物线C：y=x2经过变化可得到抛物线C1：y1=a1x（x-b1），C1与x轴的正半轴交与点A1，且其对称轴分别交抛物线C，C1于点B1，D1，此时四边形OB1A1D1恰为正方形；按上述类似方法，如图2，抛物线C1：y1=a1x（x-b1）经过变换可得到抛物线C2：y2=a2x（x-b2），C2与x轴的正半轴交与点A2，且其对称轴分别交抛物线C1，C2于点B2，D2，此时四边形OB2A2D2也恰为正方形；按上述类似方法，如图3，可得到抛物线C3：y3=a3x（x-b3）与正方形OB3A3D3．请探究以下问题：
（1）填空：a1=1，b1=2；
（2）求出C2与C3的解析式；
（3）按上述类似方法，可得到抛物线Cn：yn=anx（x-bn）与正方形OBnAnDn（n≥1）．
①请用含n的代数式直接表示出Cn的解析式；
②当x取任意不为0的实数时，试比较y2015与y2016的函数值的大小并说明理由．
16．某商店购买60件A商品和30件B商品共用了1080元，购买50件A商品和20件B商品共用了880元．
（1）A、B两种商品的单价分别是多少元？
（2）已知该商店购买B商品的件数比购买A商品的件数的2倍少4件，如果需要购买A、B两种商品的总件数不少于32件，且该商店购买的A、B两种商品的总费用不超过296元，那么该商店有哪几种购买方案？
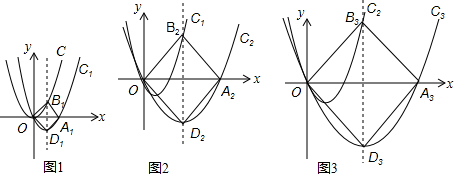
17．如图，在△ABC中，AB=10，∠B=60°，点D、E分别在AB、BC上，且BD=BE=4，将△BDE沿DE所在直线折叠得到△B′DE（点B′在四边形ADEC内），连接AB′，则AB′的长为2$\sqrt{7}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网