题目内容
4.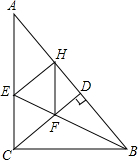 已知:如图,△ABC中,∠ACB=90°,BE平分∠ABC,CD⊥AB于D,EH⊥AB于H,CD交BE于F.求证:
已知:如图,△ABC中,∠ACB=90°,BE平分∠ABC,CD⊥AB于D,EH⊥AB于H,CD交BE于F.求证:(1)CE=CF;
(2)四边形CEHF为菱形.
分析 (1)根据角平分线性质求出CE=EH,求出CE=CF;
(2)首先推出EH∥CF,EH=CF,得出平行四边形CEHF,根据菱形的判定推出即可.
解答 证明:(1))∵BE平分∠CBA,
∴∠CBE=∠HBE,
∵∠ACB=90°,CD⊥AB,
∴∠ACB=∠BDF,
∵∠EFC=∠DFB=90°-∠HBE,∠CEF=90°-∠CBE,
∴∠CEF=∠CFE,
∴CE=CF;
(2)∵CE=CF,
∵BE平分∠CBA,∠ACB=90°,EH⊥AB,
∴CE=EH,
∴CF=EH,
∵EH⊥AB,CD⊥AB,
∴CF∥EH,
∵CF=EH,CF=CE,
∴四边形CEHF是菱形.
点评 本题考查了平行四边形的判定,菱形的判定,角平分线性质,等腰三角形的判定的应用,解此题的关键是推出CF=EH,题目综合性比较强,有一定的难度.

练习册系列答案
相关题目
14.计算:5-2等于( )
| A. | -25 | B. | 25 | C. | -$\frac{1}{25}$ | D. | $\frac{1}{25}$ |
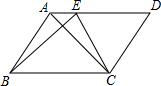 已知,如图,?ABCD中,E是边AD上任意一点,求证:S△ABC=S△EBC.
已知,如图,?ABCD中,E是边AD上任意一点,求证:S△ABC=S△EBC.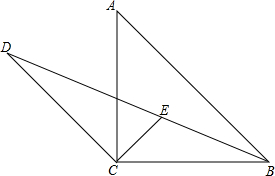 在△ABC中,∠ACB=90°,AC=BC,过C作CD∥AB交∠ABC的平分线于点D,∠ACB的平分线交BD于点E.
在△ABC中,∠ACB=90°,AC=BC,过C作CD∥AB交∠ABC的平分线于点D,∠ACB的平分线交BD于点E.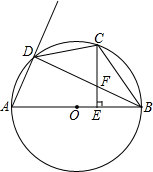 如图,AB是⊙O的直径,C是弧BD的中点,CE⊥AB,垂足为E,BD交CE于点F.
如图,AB是⊙O的直径,C是弧BD的中点,CE⊥AB,垂足为E,BD交CE于点F.