题目内容
1.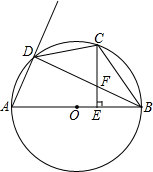 如图,AB是⊙O的直径,C是弧BD的中点,CE⊥AB,垂足为E,BD交CE于点F.
如图,AB是⊙O的直径,C是弧BD的中点,CE⊥AB,垂足为E,BD交CE于点F.(1)求证:CF=BF;
(2)若BE=4,EF=3,求⊙O的半径.
分析 (1)连AC,由AB是⊙O的直径,则∠ACB=90°,而CE⊥AB,所以∠BAC=∠BCE;由C是弧BD的中点,得到∠DBC=∠BAC,于是∠BCE=∠DBC,即可得到CF=BF.
(2)由勾股定理得BF=CF=5,则CE=8,由相似三角形性质得CE2=BE•AB,代入求出AB的值,得出半径.
解答 (1)证明:连接AC,如图,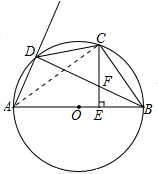
∵C是弧BD的中点,
∴∠DBC=∠BAC,
在ABC中,∠ACB=90°,CE⊥AB,
∴∠BCE+∠ECA=∠BAC+∠ECA=90°,
∴∠BCE=∠BAC,
又C是弧BD的中点,
∴∠DBC=∠CDB,
∴∠BCE=∠DBC,
∴CF=BF.
(2)解:∵BE=4,EF=3,
∴BF=$\sqrt{{3}^{2}{+4}^{2}}$=5,
∴CF=5,
∴CE=8,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴CE2=BE•AB,
∴AB=$\frac{{CE}^{2}}{BE}$=$\frac{64}{4}$=16,
∴AO=8,
∴圆O的半径为8.
点评 本题主要考查了圆周角定理,勾股定理,相似三角形的性质等,利用圆周角定理和相似三角形的性质是解此题的关键.

练习册系列答案
相关题目
 如图,在?BFDE中,分别延长DF到C、BE到A,使得DF=FC、BE=EA.求证:四边形ABCD是平行四边形.
如图,在?BFDE中,分别延长DF到C、BE到A,使得DF=FC、BE=EA.求证:四边形ABCD是平行四边形.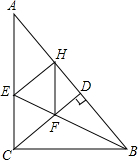 已知:如图,△ABC中,∠ACB=90°,BE平分∠ABC,CD⊥AB于D,EH⊥AB于H,CD交BE于F.求证:
已知:如图,△ABC中,∠ACB=90°,BE平分∠ABC,CD⊥AB于D,EH⊥AB于H,CD交BE于F.求证:
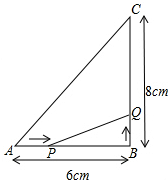 如图所示,△ABC中,∠B=90°,AB=6cm,BC=8cm.
如图所示,△ABC中,∠B=90°,AB=6cm,BC=8cm.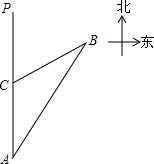 一船以每小时36海里的速度向正北航行到A处,发现它的北偏东30°方向上有一灯塔B,船继续向北航行40分钟后到达C处,发现灯塔B在北偏东60°方向上,求此船与灯塔的距离.
一船以每小时36海里的速度向正北航行到A处,发现它的北偏东30°方向上有一灯塔B,船继续向北航行40分钟后到达C处,发现灯塔B在北偏东60°方向上,求此船与灯塔的距离.