题目内容
2.解下列方程组(1)$\left\{\begin{array}{l}{x:y=3:2}\\{y:z=5:4}\end{array}\right.$.
(2)$\left\{\begin{array}{l}{x+y=1}\\{y+z=6}\\{z+x=3}\end{array}\right.$.
(3)$\left\{\begin{array}{l}{2x+3y+z=6}\\{x-y+2z=-1}\\{x+2y-z=5}\end{array}\right.$.
分析 (1)把z看做已知数表示出x与y即可;
(2)方程组三个方程相加求出x+y+z=10,把每个方程代入求出x,y,z的值即可;
(3)方程组利用加减消元法求出解即可.
解答 解:(1)方程组整理得:$\left\{\begin{array}{l}{2x=3y①}\\{4y=5z②}\end{array}\right.$,
由①得:y=$\frac{2}{3}$x③,
把③代入②得:$\frac{8}{3}$x=5z,即x=$\frac{15}{8}$z,
∴y=$\frac{5}{4}$z,
则方程组的解为$\left\{\begin{array}{l}{x=\frac{15}{8}z}\\{y=\frac{5}{4}z}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{x+y=1①}\\{y+z=6②}\\{z+x=3③}\end{array}\right.$,
①+②+③得:2(x+y+z)=10,即x+y+z=5④,
把①代入④得:z=4;
把②代入④得:x=-1;
把③代入④得:y=2,
则方程组的解为$\left\{\begin{array}{l}{x=-1}\\{y=2}\\{z=4}\end{array}\right.$;
(3)$\left\{\begin{array}{l}{2x+3y+z=6①}\\{x-y+2z=-1②}\\{x+2y-z=5③}\end{array}\right.$,
①×2-②得:3x+7y=13④,
①+③得:3x+5y=11⑤,
④-⑤得:2y=2,即y=1,
把y=1代入④得:x=2,
把x=2,y=1代入②得:z=-1,
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=1}\\{z=-1}\end{array}\right.$.
点评 此题考查了解三元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

| A. | 平分弦的半径垂直于弦 | |
| B. | 垂直平分弦的直线必经过圆心 | |
| C. | 垂直于弦的直径平分这条弦所对的弧 | |
| D. | 平分弧的直径垂直平分这条弧所对的弦 |
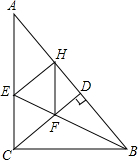 已知:如图,△ABC中,∠ACB=90°,BE平分∠ABC,CD⊥AB于D,EH⊥AB于H,CD交BE于F.求证:
已知:如图,△ABC中,∠ACB=90°,BE平分∠ABC,CD⊥AB于D,EH⊥AB于H,CD交BE于F.求证:
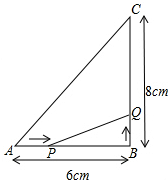 如图所示,△ABC中,∠B=90°,AB=6cm,BC=8cm.
如图所示,△ABC中,∠B=90°,AB=6cm,BC=8cm.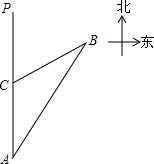 一船以每小时36海里的速度向正北航行到A处,发现它的北偏东30°方向上有一灯塔B,船继续向北航行40分钟后到达C处,发现灯塔B在北偏东60°方向上,求此船与灯塔的距离.
一船以每小时36海里的速度向正北航行到A处,发现它的北偏东30°方向上有一灯塔B,船继续向北航行40分钟后到达C处,发现灯塔B在北偏东60°方向上,求此船与灯塔的距离.