题目内容
19.如图1,等边三角形ABC中,点D在AB上(点D与点A,B不重合),DE⊥BC,垂足为E,点P在BC上,且DP∥AC,△B′DE′与△BDE关于DP对称.设BE=x,△B′DE′与△ABC重叠部分的面积为S,S关于x的函数图象如图2所示(其中0<x<$\frac{1}{2}$,$\frac{1}{2}$≤x<m与m≤x<n时,函数的解析式不同).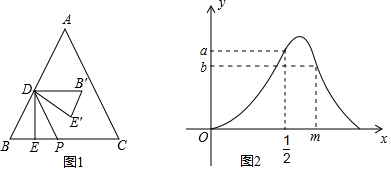
(1)填空:等边三角形ABC的边长为2,图2中a的值为$\frac{\sqrt{3}}{8}$;
(2)求S关于x的函数关系式,并直接写出x的取值范围.
分析 (1)先根据图象得到当x=BE=$\frac{1}{2}$时,点B'在AC上,进而得出△ADB'是等边三角形,根据AD=DB'=DB=1,可得等边三角形ABC的边长为2,再根据S△DB'E'=S△DBE=$\frac{\sqrt{3}}{8}$,可得a的值;
(2)分三种情况讨论:当0<x<$\frac{1}{2}$时,当$\frac{1}{2}$≤x<$\frac{2}{3}$时,当$\frac{2}{3}$≤x<1时,分别根据△B′DE′与△ABC重叠部分的形状,运用图形面积的和差关系得到S的表达式.
解答 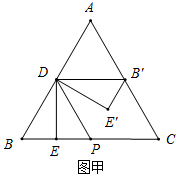 解:(1)如图甲,当x=BE=$\frac{1}{2}$时,点B'在AC上,
解:(1)如图甲,当x=BE=$\frac{1}{2}$时,点B'在AC上,
∵DE⊥BC,
∴∠BDE=30°,
∴BD=2BE=1,DE=$\frac{1}{2}\sqrt{3}$,
又∵△B′DE′与△BDE关于DP对称,DP∥AC,
∴DB'=DB=1,且∠BDB'=60°×2=120°,
∴DB'∥BC,
∴△ADB'是等边三角形,
∴AD=DB'=DB=1,
∴AB=2,即等边三角形ABC的边长为2,
∵S△DB'E'=S△DBE=$\frac{1}{2}$×$\frac{1}{2}$×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{8}$,
∴a=$\frac{\sqrt{3}}{8}$,
故答案为:2,$\frac{\sqrt{3}}{8}$;
(2)当0<x<$\frac{1}{2}$时,如图1,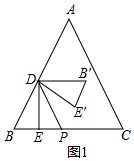
∵△ABC是等边三角形,DE⊥BC,
∴∠A=∠B=60°,∠BDE=30°,
∵△B′DE′与△BDE关于DP对称,
∴S=S△DB'E'=S△DBE=$\frac{1}{2}$BE×DE=$\frac{1}{2}$x•$\sqrt{3}$x=$\frac{\sqrt{3}}{2}$x2;
当x=m时,点E'在AC上,此时,BE=AD=$\frac{1}{3}$AB=$\frac{2}{3}$,即m=$\frac{2}{3}$,
当$\frac{1}{2}$≤x<$\frac{2}{3}$时,如图2,
设B'D,B'E'分别与AC交于点M,N,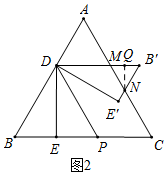
∵DP∥AC,
∴∠B'MN=∠DMA=∠MDP,∠BDP=∠A,
∵△B′DE′与△BDE关于DP对称,
∴∠MDP=∠BDP=∠A=60°,∠B'=∠B=60°,
∴∠B'MN=∠DMA=60°,
∴∠B'NM=60°=∠B'MN=∠B',∠ADM=60°=∠DMA=∠A,
∴△B'MN和△ADM都是等边三角形,
作NQ⊥B'M于Q,则NQ=$\frac{\sqrt{3}}{2}$B'N,
∵B'M=B'D-DM=BD-AD=2x-(2-2x)=4x-2,
∴S=S四边形DE'NM
=S△B'DE'-S△B'MN
=S△BDE-S△B'MN
=$\frac{\sqrt{3}}{2}$x2-$\frac{1}{2}$(4x-2)•$\frac{\sqrt{3}}{2}$(4x-2)
=-$\frac{7}{2}$x2+4$\sqrt{3}$x-$\sqrt{3}$;
当点D与点A重合时,x=BE=$\frac{1}{2}$BC=1,即n=1,
当$\frac{2}{3}$≤x<1时,如图3,
设B'D,DE'与AC分别交于点M,N,作AQ⊥DM于Q,
∵∠B'DE'=∠BDE=30°,∠ADM=60°,
∴∠ADN=90°,
∴S=S△MND
=S△ADN-S△ADM
=$\frac{1}{2}$(2-2x)•$\sqrt{3}$(2-2x)-$\frac{1}{2}$(2-2x)•$\frac{\sqrt{3}}{2}$(2-2x)
=$\sqrt{3}$x2-2$\sqrt{3}$x+$\sqrt{3}$.
综上所述,S关于x的函数关系式为:S=$\left\{\begin{array}{l}{\frac{\sqrt{3}}{2}{x}^{2}(0<x<\frac{1}{2})}\\{-\frac{7}{2}\sqrt{3}{x}^{2}+4\sqrt{3}x-\sqrt{3}(\frac{1}{2}≤x<\frac{2}{3})}\\{\sqrt{3}{x}^{2}-2\sqrt{3}x+\sqrt{3}(\frac{2}{3}≤x<1)}\end{array}\right.$
点评 本题主要考查了动点问题的函数图象以及等边三角形的性质的运用,解决问题的关键是依据题意画出图形,分情况进行讨论,解题时注意:根据0<x<$\frac{1}{2}$,$\frac{1}{2}$≤x<m与m≤x<n时函数的解析式不同,可得分段函数.

 为了让更多的失学儿童重返校园,某社区组织“献爱心手拉手”捐款活动.对社区部分捐款户数进行调查和分组统计后,将数据整理成如图所示的统计图(图中信息不完整).已知A、B两组捐款户数的比为1:5.
为了让更多的失学儿童重返校园,某社区组织“献爱心手拉手”捐款活动.对社区部分捐款户数进行调查和分组统计后,将数据整理成如图所示的统计图(图中信息不完整).已知A、B两组捐款户数的比为1:5.捐款户数分组统计表
| 组别 | 捐款额(x)元 | 户数 |
| A | 1≤x<100 | a |
| B | 100≤x<200 | 10 |
| C | 200≤x<300 | |
| D | 300≤x<400 | |
| E | x≥400 |
(1)a=2,本次调查样本的容量是50;
(2)补全“捐款户数分组统计图1”,“捐款户数分组统计图2”中B组扇形圆心角度数为72°;
(3)若该社区有500户住户,请根据以上信息,估计全社区捐款不少于300元的户数180户.
 某校组织学生排球垫球训练,训练前后,对每个学生进行考核.现随机抽取部分学生,统计了训练前后两次考核成绩,并按“A,B,C”三个等次绘制了如图不完整的统计图.试根据统计图信息,解答下列问题:
某校组织学生排球垫球训练,训练前后,对每个学生进行考核.现随机抽取部分学生,统计了训练前后两次考核成绩,并按“A,B,C”三个等次绘制了如图不完整的统计图.试根据统计图信息,解答下列问题: