题目内容
1. 如图,AB是半圆O的直径,C是半圆O上一点,弦AD平分∠BAC,交BC于点E,若AB=6,AD=5,则DE的长为$\frac{11}{5}$.
如图,AB是半圆O的直径,C是半圆O上一点,弦AD平分∠BAC,交BC于点E,若AB=6,AD=5,则DE的长为$\frac{11}{5}$.
分析 连接BD,由勾股定理先求出BD的长,再判定△ABD∽△BED,根据对应边成比例列出比例式,可求得DE的长.
解答 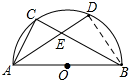 解:如图,连接BD,
解:如图,连接BD,
∵AB为⊙O的直径,AB=6,AD=5,
∴∠ADB=90°,
∴BD=$\sqrt{{6}^{2}-{5}^{2}}$=$\sqrt{11}$,
∵弦AD平分∠BAC,
∴$\widehat{CD}=\widehat{BD}$,
∴∠DBE=∠DAB,
在△ABD和△BED中,
$\left\{\begin{array}{l}{∠BAD=∠EBD}\\{∠ADB=∠BDE}\end{array}\right.$,
∴△ABD∽△BED,
∴$\frac{ED}{BD}=\frac{BD}{AD}$,即BD2=ED×AD,
∴($\sqrt{11}$)2=ED×5,
解得DE=$\frac{11}{5}$.
故答案为:$\frac{11}{5}$.
点评 此题主要考查了相似三角形的判定和性质,以及圆周角定理,解答此题的关键是作辅助线,构造出△ABD∽△BED.

练习册系列答案
相关题目
9.下列各式从左到右的变形正确的是( )
| A. | $\frac{(-a+b)^2}{(a-b)^2}$=1 | B. | $\frac{-a-1}{-a^2+8}$=$\frac{a-1}{a^2+8}$ | ||
| C. | $\frac{x^2+y^2}{x+y}$=x+y | D. | $\frac{0.5+2y}{-0.1+x}$=$\frac{5+2y}{1+x}$ |
6.下列说法:
①任意三角形的内角和都是180°;
②三角形的一个外角大于任何一个内角;
③三角形的中线、角平分线和高线都是线段;
④三角形的三条高线必在三角形内,
其中正确的是( )
①任意三角形的内角和都是180°;
②三角形的一个外角大于任何一个内角;
③三角形的中线、角平分线和高线都是线段;
④三角形的三条高线必在三角形内,
其中正确的是( )
| A. | ①② | B. | ①③ | C. | ②③ | D. | ③④ |
13.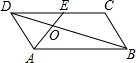 如图,在?ABCD中,E为CD的中点,AE交BD于点O,S△DCE=12,则S△AOD等于( )
如图,在?ABCD中,E为CD的中点,AE交BD于点O,S△DCE=12,则S△AOD等于( )
 如图,在?ABCD中,E为CD的中点,AE交BD于点O,S△DCE=12,则S△AOD等于( )
如图,在?ABCD中,E为CD的中点,AE交BD于点O,S△DCE=12,则S△AOD等于( )| A. | 24 | B. | 36 | C. | 48 | D. | 60 |
10.顺次连接对角线相等的四边形的四边中点所得到的四边形一定是( )
| A. | 正方形 | B. | 矩形 | C. | 菱形 | D. | 平行四边形 |
 如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,AE∥CD,CE∥AB,连接DE交AC于点O.
如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,AE∥CD,CE∥AB,连接DE交AC于点O. 如图,直线y=x-4与x轴、y轴分别交于M、N两点,⊙O的半径为2,将⊙O以每秒1个单位的速度向右作平移运动,当移动时间4-2$\sqrt{2}$或4+2$\sqrt{2}$秒时,直线MN恰好与圆相切.
如图,直线y=x-4与x轴、y轴分别交于M、N两点,⊙O的半径为2,将⊙O以每秒1个单位的速度向右作平移运动,当移动时间4-2$\sqrt{2}$或4+2$\sqrt{2}$秒时,直线MN恰好与圆相切. 如图,菱形中,对角线AC、BD交于点O,E为AD边中点,菱形ABCD的周长为32,则OE的长等于( )
如图,菱形中,对角线AC、BD交于点O,E为AD边中点,菱形ABCD的周长为32,则OE的长等于( )