题目内容
13.解不等式组:$\left\{\begin{array}{l}2x-(x-2)>4\\ \frac{1+2x}{3}≤x-1\end{array}\right.$,并在数轴上表示不等式的解集.分析 首先解不等式组中的每个不等式,然后确定两个不等式的解集的公共部分,即可确定不等式组的解集.
解答 解:$\left\{\begin{array}{l}{2x-(x-2)>4①}\\{\frac{1+2x}{3}≤x-1②}\end{array}\right.$
由不等式①得,x>2,
于不等式②得,x≥4,
把它们表示在数轴上:
∴不等式组的解集为x≥4
点评 本题考查了解一元一次不等式,在数轴上表示不等式组的解集,解一元一次不等式组的应用,解此题的关键是能求出不等式组的解集.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
3.下列根式中,最简二次根式是( )
| A. | $\sqrt{25a}$ | B. | $\sqrt{{x}^{2}+{y}^{2}}$ | C. | $\sqrt{\frac{a}{2}}$ | D. | $\sqrt{0.7}$ |
 如图,已知:EF⊥BC于F点,AD⊥BC于D点,∠1=∠E,求证:AD平分∠BAC.
如图,已知:EF⊥BC于F点,AD⊥BC于D点,∠1=∠E,求证:AD平分∠BAC.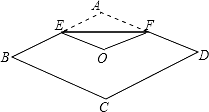 如图,将菱形纸片ABCD折叠,使点A恰好落在菱形的对称中心O处,折痕为EF,若菱形ABCD的边长为2cm,∠A=120°,则EF=$\sqrt{3}$cm.
如图,将菱形纸片ABCD折叠,使点A恰好落在菱形的对称中心O处,折痕为EF,若菱形ABCD的边长为2cm,∠A=120°,则EF=$\sqrt{3}$cm. 如图,镇江四月份某日的温度变化情况,则这天中8时到18时的温差为15.5℃.
如图,镇江四月份某日的温度变化情况,则这天中8时到18时的温差为15.5℃.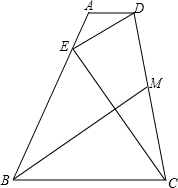 如图,在四边形ABCD中,AD∥BC,AD=AE,BE=BC,连接DE,EC
如图,在四边形ABCD中,AD∥BC,AD=AE,BE=BC,连接DE,EC