题目内容
2.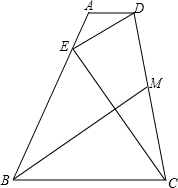 如图,在四边形ABCD中,AD∥BC,AD=AE,BE=BC,连接DE,EC
如图,在四边形ABCD中,AD∥BC,AD=AE,BE=BC,连接DE,EC(1)求证:DE⊥EC;
(2)若M为CD的中点,求证:BM∥DE.
分析 (1)分别在△AED和△BCE中表示出∠A和∠EBC的度数,然后结合∠A+∠EBC=180°求解即可;
(2)由直角三角形斜边上的中线的性质可知EM=MC,然后再根据BE=BC,可证明BM是CE的垂直平分线.
解答 证明:(1)∵AD=AE,BC=BE,
∴∠ADE=∠AED,∠BCE=∠BEC.
∴∠A=180°-2∠AED,∠ABC=180°-2∠BEC.
∵AD∥BC,
∴∠A+∠ABC=180°.
∴180°-2∠AED+180°-2∠BEC=180°.
∴∠AED+∠BEC=90°.
∴∠CDE=90°.
∴DE⊥CE.
(2)如图所示:连接EM.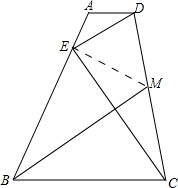
∵∠CDE=90°,M是CD的中点,
∴CM=EM.
∵BE=BC,∠CM=EM,
∴BM垂直平分CE.
∵BM⊥CE,DE⊥EC,
∴DE∥MB.
点评 本题主要考查的是线段垂直平分线的判定、直角三角形斜边上中线的性质、等腰三角形的性质、平行线的性质,证得BM是CE的垂直平分线是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.解分式方程$\frac{x}{3+x}$-$\frac{2}{2+x}$=1时,去分母后可得到( )
| A. | x(2+x)-2( 3+x)=1 | B. | x(2+x)-2=2+x | ||
| C. | x(2+x)-2( 3+x)=(2+x)(3+x) | D. | x-2( 3+x)=3+x |
7.点A(a,4)与点B(3,b)关于x轴对称,则(a+b)2013的值为( )
| A. | 0 | B. | -1 | C. | 1 | D. | 72013 |
 如图,∠FBC+∠BFD=180°,∠A=∠C,试判断AB与CE的位置关系,并说明理由.
如图,∠FBC+∠BFD=180°,∠A=∠C,试判断AB与CE的位置关系,并说明理由.