题目内容
 如图,AB、CD为⊙O的直径,
如图,AB、CD为⊙O的直径, |
| AC |
 |
| CE |
考点:圆心角、弧、弦的关系
专题:证明题
分析:先由
=
,得出AC=CE,由∠AOC=∠BOD得出AC=BD,等量代换即可得到BD=CE.
 |
| AC |
 |
| CE |
解答:证明:∵
=
,
∴AC=CE.
∵∠AOC=∠BOD,
∴AC=BD,
∴BD=CE.
 |
| AC |
 |
| CE |
∴AC=CE.
∵∠AOC=∠BOD,
∴AC=BD,
∴BD=CE.
点评:本题考查了圆心角、弧、弦的关系定理及其推论,用到的知识点:
定理:在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
定理:在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.

练习册系列答案
相关题目
下列四个式子中,错误的是( )
| A、-3.14>-π | ||||
| B、3.5>-4 | ||||
C、-5
| ||||
| D、-0.21>-0.211 |
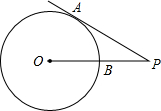 如图,点P为⊙O外一点,PA切⊙O于A,PO交⊙O于B,若PA交⊙O于B,若PA=3,PB=1,则⊙O半径为
如图,点P为⊙O外一点,PA切⊙O于A,PO交⊙O于B,若PA交⊙O于B,若PA=3,PB=1,则⊙O半径为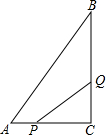 如图所示,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从C点出发沿CB边向点B以2cm/s的速度移动.如果P、Q同时出发,几秒钟后,可使△PCQ的面积为8平方厘米?
如图所示,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从C点出发沿CB边向点B以2cm/s的速度移动.如果P、Q同时出发,几秒钟后,可使△PCQ的面积为8平方厘米?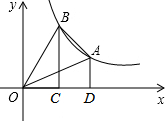 在反比例函数y=
在反比例函数y=