题目内容
5.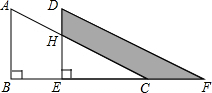 如图,直角△ABC沿点B到点C的方向平移到△DEF的位置,若AB=5,DH=1,平移距离为2,则阴影部分DHCF的面积等于4.
如图,直角△ABC沿点B到点C的方向平移到△DEF的位置,若AB=5,DH=1,平移距离为2,则阴影部分DHCF的面积等于4.
分析 根据平移的性质,得到AB=DE,BC=EF,再根据平行线分线段成比例定理,求出EC,然后用S△DEF减去S△HEC即为阴影部分DHCF的面积.
解答 解:∵AB=5,
∴DE=5,
又∵DH=1,
∴HE=5-1=4,
∵HE∥AB,
∴$\frac{HE}{AB}$=$\frac{EC}{BC}$,
即 $\frac{4}{5}$=$\frac{EC}{2+EC}$,
故EC=8,
∴S△DEF=$\frac{1}{2}$DE•EF=$\frac{1}{2}$×5×(2+8)=20;
S△HEC=$\frac{1}{2}$HE•EC=$\frac{1}{2}$×4×8=16;
∴S阴影部分DHCF=20-16=4.
故答案为4.
点评 本题考查了平移的性质:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 中的一个常数污染了.怎么办呢?小明想了一想,便翻看书后答案,此方程的解是y=-$\frac{5}{3}$,很快补好了这个常数,并迅速地完成了作业,同学们,你们能补出这个常数吗?它应是3.
中的一个常数污染了.怎么办呢?小明想了一想,便翻看书后答案,此方程的解是y=-$\frac{5}{3}$,很快补好了这个常数,并迅速地完成了作业,同学们,你们能补出这个常数吗?它应是3. 如图,P为正方形ABCD 的边AD上的一动点,AE⊥BP,CF⊥BP,垂足分别为点E、F,已知AD=4.
如图,P为正方形ABCD 的边AD上的一动点,AE⊥BP,CF⊥BP,垂足分别为点E、F,已知AD=4.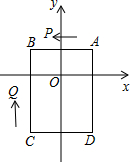 如图,已知四边形ABCD的顶点为A(1,1),B(-1,1),C(-1,-2),D(1,-2),点P从A出发同时点Q从C点出发,沿四边形的边做环绕匀速运动,P点以2单位/s的速度做逆时针运动,Q点以3单位/s的速度做顺时针运动,则点P和点Q第2017次相遇时的坐标为(0,-2).
如图,已知四边形ABCD的顶点为A(1,1),B(-1,1),C(-1,-2),D(1,-2),点P从A出发同时点Q从C点出发,沿四边形的边做环绕匀速运动,P点以2单位/s的速度做逆时针运动,Q点以3单位/s的速度做顺时针运动,则点P和点Q第2017次相遇时的坐标为(0,-2).